当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省徐州市云龙区东苑中学五校联盟九年级（上）学情检测数学试卷

发布：2024/8/26 15:0:9

一、选择题（本大题共8小题，每小题3分，共计24分）

1．关于一元二次方程x²-4x+4=0根的情况，下列判断正确的是（　　）
A．有两个不相等的实数根 B．有两个相等的实数根
C．有且只有一个实数根 D．没有实数根
组卷：346引用：7难度：0.8
解析
2．将二次函数y=（x+3）²-1图象沿x轴向右平移2个单位长度，所得抛物线对应的函数表达式为（　　）
A．y=（x+5）²-1 B．y=（x+3）²+1 C．y=（x+1）²-1 D．y=（x-1）²-3
组卷：19引用：1难度：0.5
解析
3．已知
a
b
=
2
3
，那么
a
a
+
b
的值为（　　）
A．
1
3
B．
2
5
C．
3
5
D．
3
4
组卷：3984引用：38难度：0.9
解析
4．三角形三边的长度之比为3：5：7，与它相似的三角形的最长边是21cm,另两边的长度之和是（　　）
A．15 cm B．18 cm C．21 cm D．24 cm
组卷：253引用：5难度：0.9
解析
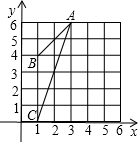5．如图中△ABC外接圆的圆心坐标是（　　）
A．（2，5） B．（5，2） C．（2，6） D．（6，2）
组卷：333引用：3难度：0.6
解析
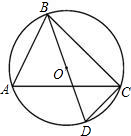6．如图，BD是⊙O的直径，∠CBD=30°，则∠A的度数为（　　）
A．30° B．45° C．60° D．75°
组卷：3616引用：58难度：0.9
解析
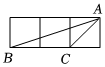7．如图，每个小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（　　）
A． B． C． D．
组卷：153引用：2难度：0.7
解析
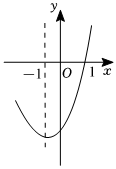8．抛物线y=ax²+bx+c的对称轴为直线x=-1，部分，下列判断中：①abc＞0；②b²-4ac＞0；③9a-3b+c=0；④若点（-0.5，y₁）（-2，y₂）均在抛物线上，则y₁＞y₂；⑤当-3＜x＜1时，y＜0．其中正确的个数有（　　）
A．2 B．3 C．4 D．5
组卷：16引用：1难度：0.4
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（大题共7小题，共86分）

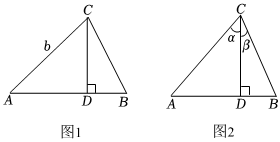24．如图（1），△ABC中，AC=b,AB=c,CD⊥AB于点D．由直角三角形边角关系，可将三角形的面积公式变形为S_△ABC=
1
2
bc•sinA①，即三角形的面积等于两边之长与夹角正弦值之积的一半．
如图（2），在△ABC中，CD⊥AB于点D，∠ACD=α，∠DCB=β，∵S_△ABC=S_△ADC+S_△BDC，由公式①，得
1
2
AC•BCsin（α+β）=
1
2
AC•CDsinα+
1
2
BC•CDsinβ，即：AC•BC•sin（α+β）=AC•CD•sinα+BC•CD•sinβ②．
（1）请证明等式：sin（α+β）=sinαcosβ+cosαsinβ；
（2）请利用结论求出sin75°的值．
组卷：64引用：1难度：0.5
解析
25．在平面直角坐标系中，二次函数y=ax²+
5
3
x+c的图象经过点C（0，2）和点D（4，-2），点E是直线y=-
1
3
x+2的图象与二次函数图象在第一象限内的交点．
（1）求二次函数的解析式；
（2）如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME，求四边形COEM面积的最大值；
（3）如图②，经过A、B、C三点的圆交y轴于点F（点F与点C不重合），请直接写出点F的坐标．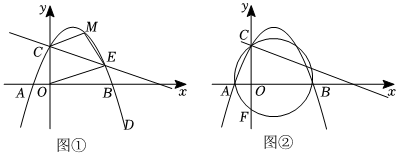
组卷：283引用：2难度：0.2
解析