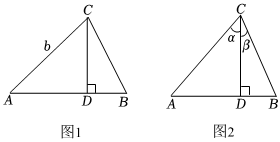
如图（1），△ABC中，AC=b,AB=c,CD⊥AB于点D．由直角三角形边角关系，可将三角形的面积公式变形为S_△ABC=

1

2

bc•sinA①，即三角形的面积等于两边之长与夹角正弦值之积的一半．
如图（2），在△ABC中，CD⊥AB于点D，∠ACD=α，∠DCB=β，∵S_△ABC=S_△ADC+S_△BDC，由公式①，得

1

2

AC•BCsin（α+β）=

1

2

AC•CDsinα+

1

2

BC•CDsinβ，即：AC•BC•sin（α+β）=AC•CD•sinα+BC•CD•sinβ②．
（1）请证明等式：sin（α+β）=sinαcosβ+cosαsinβ；
（2）请利用结论求出sin75°的值．