2022-2023学年湖北省黄冈市浠水一中高二（下）期末数学试卷

一、单项选择题（本题共8小题，每小题5分，共40分.）

• 1．集合A={x|-1≤x＜2}，B={x|x＞1}，则A∩（∁_RB）=（　　）

  A．{x|-1≤x＜1}

  B．{x|-1≤x≤1}

  C．{x|-1≤x＜2}

  D．{x|x＜2}
  组卷：334引用：12难度：0.9

  解析

• 2．已知

  f

  ′

  （

  x

  0

  ）

  =

  3

  ，

  lim

  Δ

  x

  →

  0

  f

  （

  x

  0

  +

  2

  Δ

  x

  ）

  -

  f

  （

  x

  0

  ）

  3

  Δ

  x

  的值是（　　）

  A．3

  B．1

  C．2

  D． 3 2
  组卷：84引用：5难度：0.8

  解析

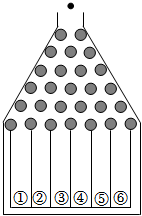• 3．如图是一块高尔顿板示意图：在一块木板上钉着若干排互相平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，小球从上方的通道口落下后，将与层层小木块碰撞，最后掉入下方的某一个球槽内，若小球下落过程中向左、向右落下的机会均等，则小球最终落入④号球槽的概率为（　　）

  A． 3 32

  B． 15 64

  C． 5 32

  D． 5 16
  组卷：206引用：9难度：0.8

  解析

• 4．若f（x）=（x+a）

  ln

  2

  x

  -

  1

  2

  x

  +

  1

  为偶函数，则a=（　　）

  A．-1

  B．0

  C． 1 2

  D．1
  组卷：5760引用：23难度：0.6

  解析

• 5．一个袋子中有3个红球和2个白球，这些小球除颜色外没有其他差异．从中不放回地抽取2个球，每次只取1个．设事件A=“第一次抽到红球”，B=“第二次抽到红球”，则概率P（B|A）是（　　）

  A． 1 2

  B． 2 5

  C． 1 4

  D． 1 5
  组卷：50引用：7难度：0.8

  解析

• 6．已知函数f（x）是定义在R上的奇函数，f（1）=5且f（x+3）=-f（x），则f（2022）+f（2023）=（　　）

  A．-5

  B．2

  C．0

  D．5
  组卷：504引用：6难度：0.7

  解析

• 7．现实世界中的很多随机变量遵循正态分布．例如反复测量某一个物理量，其测量误差X通常被认为服从正态分布．若某物理量做n次测量，最后结果的误差X_n～N（0，

  2

  n

  ），则为使

  |

  X

  n

  |

  ≥

  1

  4

  的概率控制在0.0455以下，至少要测量的次数为（　　）
  （附：若随机变量ξ服从正态分布N（μ，σ²），则P（μ-σ＜ξ≤μ+σ）≈0.6827，P（μ-2σ＜ξ≤μ+2σ）≈0.9545，P（μ-3σ＜ξ≤μ+3σ）≈0.9973）

  A．32

  B．64

  C．128

  D．256
  组卷：19引用：2难度：0.7

  解析

四、解答题（本题共6小题，共70分.）

• 21．某公司通过游戏获得积分以激励员工．游戏规则如下：甲袋和乙袋中各装有形状和大小完全相同的10个球，其中甲袋中有5个红球和5个白球，乙袋中有8个红球和2个白球，获得积分有两种方案．
  方案一：从甲袋中有放回地摸球3次，每次摸出1个球，摸出红球获得10分，摸出白球得0分；
  方案二：掷一枚质地均匀的骰子，如果点数为1或2，从甲袋中随机摸出1个球；如果点数为3，4，5，6，从乙袋中随机摸出一个球，若摸出的是红球，则获得积分15分，否则得5分．
  （1）某员工获得1次游戏机会，若以积分的均值为依据，请判断该员工应该选择方案一还是方案二？
  （2）若某员工获得10次游戏机会，全部选择方案一，记该员工摸出红球的次数为Y，当P（Y=k）取得最大值时，求k的值．
  组卷：113引用：2难度：0.6

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  lnx

  +

  a

  x

  （

  a

  ∈

  R

  ）

  ．
  （1）讨论f（x）的单调性；
  （2）函数g（x）=xf（x）-ax²-x有两个不同的极值点x₁，x₂（x₁＜x₂），证明：lnx₁+2lnx₂＞3．
  组卷：76引用：3难度：0.4

  解析