2023-2024学年天津市北辰区高二（上）期中数学试卷

一、选择题．（本大题共9个小题，每小题4分，共36分，在每小题的四个选项中，只有一项是正确的，请把它选出并填在答题卡上）

• 1．已知向量

  a

  =

  （

  3

  ，-

  2

  ，

  1

  ）

  ，

  b

  =

  （

  -

  1

  ，

  1

  ，

  4

  ）

  ，则

  a

  +

  b

  =（　　）

  A．（2，-1，3）

  B．（-2，-1，5）

  C．（-2，-3，3）

  D．（2，-1，5）
  组卷：66引用：1难度：0.7

  解析

• 2．直线

  3

  x+3y-2=0的倾斜角为（　　）

  A．150°

  B．120°

  C．60°

  D．30°
  组卷：104引用：11难度：0.9

  解析

• 3．过点（0，1）且与直线2x-y+1=0垂直的直线方程是（　　）

  A．x-2y+1=0

  B．x+2y-2=0

  C．2x+y-2=0

  D．x-2y-1=0
  组卷：78引用：1难度：0.7

  解析

• 4．若方程x²+y²+2y+2a-1=0表示圆，则实数a的取值范围为（　　）

  A．a＜1

  B．a＞1

  C．a≤0

  D．a＞0
  组卷：111引用：1难度：0.7

  解析

• 5．已知椭圆

  x

  2

  10

  -

  m

  +

  y

  2

  m

  -

  2

  =

  1

  ，焦点在y轴上，且焦距为4，则短轴长为（　　）

  A． 2 2

  B．4

  C． 4 2

  D．8
  组卷：181引用：2难度：0.7

  解析

• 6．若直线l₁：（a-2）x+ay+4=0与l₂：（a-2）x+3y+2a=0平行，则a的值为（　　）

  A．0

  B．2

  C．3

  D．2或3
  组卷：105引用：2难度：0.8

  解析

三、解答题．（本大题共5个小题，共60分）

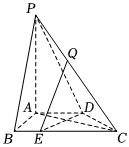• 19．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，其中AD∥BC，AB⊥AD，AB=AD=

  1

  2

  BC=2，PA=4，E为棱BC上的点，且BE=

  1

  4

  BC．
  （1）求证：DE⊥平面PAC；
  （2）求点E到平面PCD的距离；
  （3）设Q为棱CP上的点（不与C，P重合），且直线QE与平面PAC所成角的正弦值为

  5

  5

  ，求

  CQ

  CP

  的值．
  组卷：47引用：2难度：0.5

  解析

• 20．已知椭圆N：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）经过点C（0，1），且离心率为

  2

  2

  ．
  （1）求椭圆N的方程；
  （2）直线l：y=kx-

  1

  3

  与椭圆N的交点为A，B两点，线段AB的中点为M，是否存在常数λ，使∠AMC=λ•∠ABC恒成立，并说明理由．
  组卷：146引用：4难度：0.4

  解析