2023-2024学年北京市海淀区民大附中八年级（上）期中数学试卷

一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）

• 1．在平面直角坐标系xOy中，点P（-3，5）关于y轴对称的点的坐标是（　　）

  A．（-3，-5）

  B．（3，-5）

  C．（3，5）

  D．（5，-3）
  组卷：248引用：18难度：0.9

  解析

• 2．在下列长度的四根木棒中，能与3cm,8cm长的两根木棒钉成一个三角形的是（　　）

  A．3cm

  B．5cm

  C．7cm

  D．12cm
  组卷：344引用：11难度：0.6

  解析

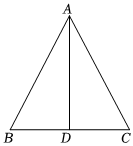• 3．如图，在△ABC中，AB=AC，AD是△ABC的边BC上的中线，那么可以证明△ABD≌△ACD，这里证明全等所使用的判定方法是（　　）

  A．SAS

  B．AAS

  C．ASA

  D．SSS
  组卷：83引用：3难度：0.6

  解析

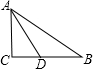• 4．如图，∠C=90°，AD平分∠BAC交BC于D，若BC=5cm,BD=3cm,则点D到AB的距离为（　　）

  A．5cm

  B．3cm

  C．2cm

  D．不能确定
  组卷：366引用：20难度：0.9

  解析

• 5．如图所示，AB=AC，AD=AE，∠BAC=∠DAE，B、D、E三点共线，∠1=25°，∠2=30°，则∠3=（　　）

  A．60°

  B．55°

  C．50°

  D．无法计算
  组卷：1023引用：23难度：0.7

  解析

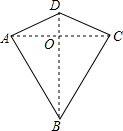• 6．两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，詹姆斯在探究筝形的性质时，得到如下结论：
  ①AC⊥BD；②AO=CO=

  1

  2

  AC；③△ABD≌△CBD，
  其中正确的结论有（　　）

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：5167引用：87难度：0.9

  解析

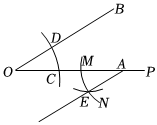• 7．如图，已知∠BOP与OP上的点C，点A，小临同学现进行如下操作：①以点O为圆心，OC长为半径画弧，交OB于点D，连接CD；②以点A为圆心，OC长为半径画弧，交OA于点M；③以点M为圆心，CD长为半径画弧，交第2步中所画的弧于点E，连接ME．下列结论不能由上述操作结果得出的是（　　）

  A．∠ODC=∠AEM

  B．OB∥AE

  C．∠AME=2∠AOD

  D．CD∥ME
  组卷：457引用：12难度：0.7

  解析

• 8．如图1，△ABC中，AB=AC，D为BC中点，把△ABC纸片沿AD对折得到△ADC，如图2，点E和点F分别为AD，AC上的动点，把△ADC纸片沿EF折叠，使得点A落在△ADC的外部，如图3所示．设∠1-∠2=α，则下列等式成立的是（　　）
  

  A．∠BAC=α

  B．2∠BAC=α

  C．∠BAC=2α

  D．3∠BAC=2α
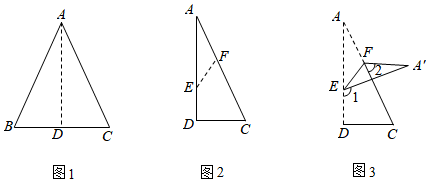  组卷：439引用：9难度：0.7

  解析

三、解答题（本大题共8小题，共60.0分。解答应写出文字说明，证明过程或演算步骤）

• 23．在△ABC中，AC=BC，∠ACB=90°，点D在BC的延长线上，M是BD的中点，E是射线CA上一动点，且CE=CD，连接AD，作DF⊥AD，DF交EM延长线于点F．
  
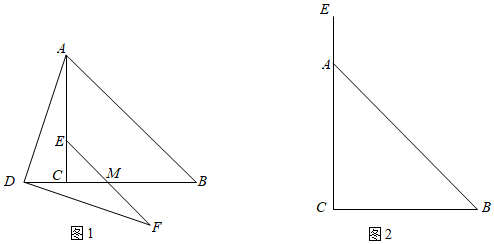
  （1）如图1，当点E在CA上时，填空：AD

  DF（填“=”、“＜”或“＞”）．
  （2）如图2，当点E在CA的延长线上时，请根据题意将图形补全，判断AD与DF的数量关系，并证明你的结论．
  组卷：1000引用：13难度：0.5

  解析

• 24．小聪和小明两位同学在学习全等三角形时积极思考，提出了以下两个问题：
  问题1：如图1，△ABC中，AB=3，AC=2，AD是△ABC的角平分线，求BD：DC的值．
  小聪同学经过思考，发现可以过D作DM⊥AB于M，DN⊥AC于N，利用△ABD与△ACD的面积比来解决这个问题．
  问题2：如图2，△ABC为等边三角形，点D为△ABC外一点，∠CDA=60°，连接DB，探究AD，CD，BD三者之间的数量关系．
  小明同学经过思考，发现可以在DA上截取DE=DC，构造等边三角形CDE，从而解决这个问题．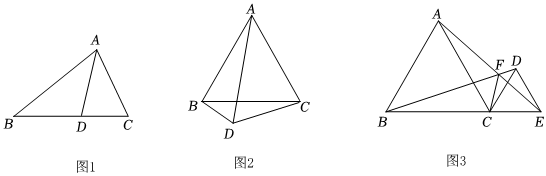
  
  （1）根据两位同学的思考，完成问题1、2的解答（直接写出结果）．
  （2）根据问题1、2的结论，解决下面问题：如图3，△ABC和△CDE都是等边三角形，且B、C、E三点共线，连接AE，BD交于点F，连接FC，设AF=a,DF=b,CF=c,若BC=2CE，直接写出

  a

  -

  2

  b

  3

  c

  的值．
  组卷：500引用：4难度：0.4

  解析