当前位置：试卷中心 > 试卷详情

2021-2022学年四川省成都七中高二（下）零诊模拟数学试卷（理科）（6月份）

发布：2024/8/16 5:0:1

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设非空集合M，N满足M∪N=N，则（　　）
A．∀x∈N，x∈M B．∀x∉N，有x∉M
C．∃x₀∉M，有x₀∈N D．∃x₀∈N，有x₀∉M
组卷：28引用：4难度：0.8
解析
2．若复数z满足（1-i）z=1+2i,则
z
在复平面内对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：174引用：10难度：0.9
解析
3．已知
OA
，
OB
，
OC
均为单位向量，且满足
1
2
OA
+
OB
+
OC
=
0
，则
AB
•
AC
的值为（　　）
A．
3
8
B．
5
8
C．
7
8
D．
19
8
组卷：389引用：6难度：0.7
解析
4．数列{a_n}满足
a
n
+
1
=
-
a
2
n
+
a
n
（n∈N^*），
a
1
∈
（
0
，
1
2
）
，则以下说法正确的个数（　　）
①0＜a_n+1＜a_n；
②
a
2
1
+
a
2
2
+
a
2
3
+
…
+
a
2
n
＜
a
1
；
③对任意正数b,都存在正整数m使得
1
1
-
a
1
+
1
1
-
a
2
+
1
1
-
a
3
+
…
+
1
1
-
a
m
＞
b
成立；
④
a
n
＜
1
n
+
1
．
A．1 B．2 C．3 D．4
组卷：24引用：1难度：0.6
解析
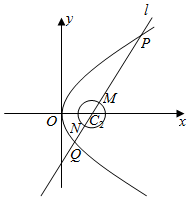5．如图，已知抛物线C₁的顶点在坐标原点，焦点在x轴上，且过点（3，6），圆C₂：x²+y²-6x+8=0，过圆心C₂的直线l与抛物线和圆分别交于P，Q，M，N，则|PN|+3|QM|的最小值为（　　）
A．12+4
3
B．16+4
3
C．16+6
3
D．20+6
3
组卷：722引用：7难度：0.4
解析
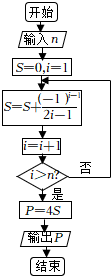6．德国数学家莱布尼兹（1646年-1716年）于1674年得到了第一个关于π的级数展开式，该公式于明朝初年传入我国．在我国科技水平业已落后的情况下，我国数学家、天文学家明安图（1692年-1765年）为提高我国的数学研究水平，从乾隆初年（1736年）开始，历时近30年，证明了包括这个公式在内的三个公式，同时求得了展开三角函数和反三角函数的6个新级数公式，著有《割圆密率捷法》一书，为我国用级数计算π开创了先河．如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值（其中P表示π的近似值），若输入n=10，则输出的结果是（　　）
A．
P
=
4
（
1
-
1
3
+
1
5
-
1
7
+
…
+
1
17
）
B．
P
=
4
（
1
-
1
3
+
1
5
-
1
7
+
…-
1
19
）
C．
P
=
4
（
1
-
1
3
+
1
5
-
1
7
+
…
+
1
21
）
D．
P
=
4
（
1
-
1
3
+
1
5
-
1
7
+
…-
1
21
）
组卷：49引用：12难度：0.7
解析
7．在正四面体ABCD中，异面直线AB与CD所成的角为α，直线AB与平面BCD所成的角为β，二面角C-AB-D的平面角为γ，则α，β，γ的大小关系为（　　）
A．β＜α＜γ B．α＜β＜γ C．γ＜β＜α D．β＜γ＜α
组卷：132引用：3难度：0.4
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

[选修4—4：坐标系与参数方程]

22．在直角坐标系xOy中，倾斜角为α的直线l的参数方程为
x
=
2
+
tcosα
，
y
=
3
+
tsinα
（t为参数）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ²=2ρcosθ+8．
（1）求直线l的普通方程与曲线C的直角坐标方程；
（2）若直线l与曲线C交于A，B两点，且|AB|=4
2
，求直线l的倾斜角．
组卷：387引用：13难度：0.5
解析

[选修4—5：不等式选讲]

23．已知函数f（x）=m-|x-2|，m∈R，g（x）=|x+3|．
（Ⅰ）当x∈R时，有f（x）≤g（x），求实数m的取值范围．
（Ⅱ）若不等式f（x）≥0的解集为[1，3]，正数a,b满足ab-2a-b=3m-1，求a+b的最小值．
组卷：86引用：7难度：0.6
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．∀x∈N，x∈M	B．∀x∉N，有x∉M
C．∃x₀∉M，有x₀∈N	D．∃x₀∈N，有x₀∉M

2021-2022学年四川省成都七中高二（下）零诊模拟数学试卷（理科）（6月份）

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设非空集合M，N满足M∪N=N，则（ ）

2．若复数z满足（1-i）z=1+2i,则z在复平面内对应的点位于（ ）

3．已知OA，OB，OC均为单位向量，且满足12OA+OB+OC=0，则AB•AC的值为（ ）

4．数列{an}满足an+1=-a2n+an（n∈N*），a1∈（0，12），则以下说法正确的个数（ ）①0＜an+1＜an；②a21+a22+a23+…+a2n＜a1；③对任意正数b,都存在正整数m使得11-a1+11-a2+11-a3+…+11-am＞b成立；④an＜1n+1．

5．如图，已知抛物线C1的顶点在坐标原点，焦点在x轴上，且过点（3，6），圆C2：x2+y2-6x+8=0，过圆心C2的直线l与抛物线和圆分别交于P，Q，M，N，则|PN|+3|QM|的最小值为（ ）

7．在正四面体ABCD中，异面直线AB与CD所成的角为α，直线AB与平面BCD所成的角为β，二面角C-AB-D的平面角为γ，则α，β，γ的大小关系为（ ）

[选修4—4：坐标系与参数方程]

[选修4—5：不等式选讲]

23．已知函数f（x）=m-|x-2|，m∈R，g（x）=|x+3|．（Ⅰ）当x∈R时，有f（x）≤g（x），求实数m的取值范围．（Ⅱ）若不等式f（x）≥0的解集为[1，3]，正数a,b满足ab-2a-b=3m-1，求a+b的最小值．

1．设非空集合M，N满足M∪N=N，则（　　）

2．若复数z满足（1-i）z=1+2i,则
z
在复平面内对应的点位于（　　）

3．已知
OA
，
OB
，
OC
均为单位向量，且满足
1
2
OA
+
OB
+
OC
=
0
，则
AB
•
AC
的值为（　　）

5．如图，已知抛物线C₁的顶点在坐标原点，焦点在x轴上，且过点（3，6），圆C₂：x²+y²-6x+8=0，过圆心C₂的直线l与抛物线和圆分别交于P，Q，M，N，则|PN|+3|QM|的最小值为（　　）

7．在正四面体ABCD中，异面直线AB与CD所成的角为α，直线AB与平面BCD所成的角为β，二面角C-AB-D的平面角为γ，则α，β，γ的大小关系为（　　）

23．已知函数f（x）=m-|x-2|，m∈R，g（x）=|x+3|．
（Ⅰ）当x∈R时，有f（x）≤g（x），求实数m的取值范围．
（Ⅱ）若不等式f（x）≥0的解集为[1，3]，正数a,b满足ab-2a-b=3m-1，求a+b的最小值．