当前位置：试卷中心 > 试卷详情

2023-2024学年贵州省高三（上）入学数学试卷

发布：2024/7/25 8:0:9

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知复数z=-1+2i（i为虚数单位），则zi=（　　）
A．-1-2i B．2-i C．-2-i D．1+2i
组卷：19引用：5难度：0.8
解析
2．若集合A={1，2，3}，集合B={z|z=x-y,x∈A，y∈A}，则集合A∪B=（　　）
A．{1，2} B．{1，2，3}
C．{-2，-1，0，1，2} D．{-2，-1，0，1，2，3}
组卷：101引用：4难度：0.8
解析
3．已知函数f（x）=e^x+x³f'（1），则f（1）=（　　）
A．e B．-e C．
e
2
D．
-
e
2
组卷：280引用：5难度：0.8
解析
4．“积跬步以至千里，积小流以成江海．”出自荀子《劝学篇》．原文为“故不积跬步，无以至千里；不积小流，无以成江海．”数学上这样的两个公式：①1.01³⁰≈1.3；②1.01³⁶⁵≈37.8，也能说明这种积少成多，聚沙成塔的成功之道．它们所诠释的含义是“每天增加1%，就会在一个月、一年以后产生巨大的变化．虽然这是一种理想化的模型，但也能充分地说明“小小的改变和时间积累的力量”．假设某同学通过学习和思考所带来的知识积累的变化，以每天2.01%的速度“进步”，则30天以后他的知识积累约为原来的（　　）
A．1.69倍 B．1.96倍 C．1.78倍 D．2.8倍
组卷：14引用：2难度：0.6
解析
5．已知函数f（x）为奇函数，g（x）为偶函数，且f（x）=g（x）-e^x，记h（x）=
f
（
x
）
g
（
x
）
，则h（1）=（　　）
A．
e
2
+
1
e
2
-
1
B．
e
2
-
1
e
2
+
1
C．
1
-
e
2
1
+
e
2
D．
1
+
e
2
1
-
e
2
组卷：66引用：2难度：0.6
解析
6．已知F为双曲线C：
x
2
a
2
-
y
2
b
2
=
1
（a＞0，b＞0）的右焦点，过点F作x轴的垂线与双曲线及它的渐近线在第一象限内依次交于点A和点B．若|AB|=|AF|，则双曲线C的渐近线方程为（　　）
A．
3
x
±
y
=
0
B．
x
±
3
y
=
0
C．
2
x
±
y
=
0
D．
x
±
2
y
=
0
组卷：71引用：3难度：0.5
解析
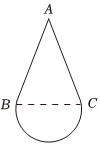7．已知“水滴”的表面是一个由圆锥的侧面和部分球面（常称为“球冠”）所围成的几何体．如图所示，将“水滴”的轴截面看成由线段AB，AC和优弧BC所围成的平面图形，其中点B，C所在直线与水平面平行，AB和AC与圆弧相切．已知“水滴”的“竖直高度”与“水平宽度”（“水平宽度”指的是平行于水平面的直线截轴截面所得线段的长度的最大值）的比值为
4
3
，则sin∠BAC=（　　）
A．
3
25
B．
9
25
C．
16
25
D．
24
25
组卷：97引用：6难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤．

21．定义：若椭圆
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的两个点A（x₁，y₁），B（x₂，y₂）满足
x
1
x
2
a
2
+
y
1
y
2
b
2
=
0
，则称A，B为该椭圆的一个“共轭点对”，记作[A，B]．已知椭圆C：
x
2
12
+
y
2
4
=1上一点A（3，1）．
（1）求“共轭点对”[A，B]中点B所在直线l的方程．
（2）设O为坐标原点，点P，Q在椭圆C上，且PQ∥OA．
①求（1）中的直线l和椭圆C的两个交点B₁，B₂的坐标；
②设四点B₁，P，B₂，Q在椭圆C上逆时针排列，证明：四边形B₁PB₂Q的面积小于8
3
．
组卷：25引用：4难度：0.4
解析
22．定义函数f（x）=（x-a）sinx,其中x∈R．
（1）当
a
=
π
6
时，求曲线y=f（x）在点
（
π
6
，
0
）
处的切线方程；
（2）证明：在区间
（
-
π
2
，
3
π
2
）
上，f（x）有且只有两个不同的极值点．
组卷：17引用：2难度：0.4
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．{1，2}	B．{1，2，3}
C．{-2，-1，0，1，2}	D．{-2，-1，0，1，2，3}

2023-2024学年贵州省高三（上）入学数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知复数z=-1+2i（i为虚数单位），则zi=（ ）

2．若集合A={1，2，3}，集合B={z|z=x-y,x∈A，y∈A}，则集合A∪B=（ ）

3．已知函数f（x）=ex+x3f'（1），则f（1）=（ ）

5．已知函数f（x）为奇函数，g（x）为偶函数，且f（x）=g（x）-ex，记h（x）=f（x）g（x），则h（1）=（ ）

6．已知F为双曲线C：x2a2-y2b2=1（a＞0，b＞0）的右焦点，过点F作x轴的垂线与双曲线及它的渐近线在第一象限内依次交于点A和点B．若|AB|=|AF|，则双曲线C的渐近线方程为（ ）

四、解答题：本题共6小题，共70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤．

22．定义函数f（x）=（x-a）sinx,其中x∈R．（1）当a=π6时，求曲线y=f（x）在点（π6，0）处的切线方程；（2）证明：在区间（-π2，3π2）上，f（x）有且只有两个不同的极值点．

1．已知复数z=-1+2i（i为虚数单位），则zi=（　　）

2．若集合A={1，2，3}，集合B={z|z=x-y,x∈A，y∈A}，则集合A∪B=（　　）

3．已知函数f（x）=e^x+x³f'（1），则f（1）=（　　）

5．已知函数f（x）为奇函数，g（x）为偶函数，且f（x）=g（x）-e^x，记h（x）=
f
（
x
）
g
（
x
）
，则h（1）=（　　）

6．已知F为双曲线C：
x
2
a
2
-
y
2
b
2
=
1
（a＞0，b＞0）的右焦点，过点F作x轴的垂线与双曲线及它的渐近线在第一象限内依次交于点A和点B．若|AB|=|AF|，则双曲线C的渐近线方程为（　　）

22．定义函数f（x）=（x-a）sinx,其中x∈R．
（1）当
a
=
π
6
时，求曲线y=f（x）在点
（
π
6
，
0
）
处的切线方程；
（2）证明：在区间
（
-
π
2
，
3
π
2
）
上，f（x）有且只有两个不同的极值点．