2022-2023学年河南省开封市五县联考高一（下）第二次月考数学试卷

一、单选题（本大题共8小题，共40分）

• 1．设（1+2i）（a+i）的实部与虚部相等，其中a为实数，则a等于（　　）

  A．-3

  B．-2

  C．2

  D．3
  组卷：5037引用：18难度：0.9

  解析

• 2．下列结论正确的是（　　）

  A．底面是正三角形的三棱锥是正三棱锥

  B．所有几何体的表面都能展开成平面图形

  C．棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥

  D．一个直角三角形绕其一条直角边所在直线旋转形成的封闭曲面所围成的图形叫做圆锥
  组卷：42引用：1难度：0.5

  解析

• 3．某学校共有980名学生，其中高一的学生有400名，高二的学生有300名，其余都是高三的学生，为了解该校学生的体育锻炼时间，按照高一、高二、高三三个级段进行分层抽样，如果样本容量为196，那么应在高三的学生中抽取（　　）

  A．48名

  B．52名

  C．56名

  D．60名
  组卷：55引用：3难度：0.7

  解析

• 4．《九章算术》是我国数学史上堪与欧几里得《几何原本》相媲美的数学名著，其第五卷《商功》中有如下问题：“今有圆堡，周四丈八尺，高一丈一尺，问积几何？“这里所说的圆堡就是圆柱体，其底面周长是4丈8尺，高1丈1尺，问它的体积是多少？若π取3，估算该圆堡的体积为（　　）立方尺（1丈=10尺）．

  A．1998

  B．2012

  C．2112

  D．2324
  组卷：31引用：1难度：0.9

  解析

• 5．m,n为空间中两条不重合直线，α为空间中一平面，则下列说法正确的是（　　）

  A．若m∥n,n⊂α，则m∥α	B．若m⊥α，m∥n,则n⊥α
  C．若m∥α，n⊂α，则m∥n	D．若m⊥α，m⊥n,则n∥α
  组卷：66引用：7难度：0.7

  解析

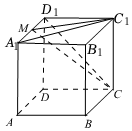• 6．如图，在正方体ABCD-A₁B₁C₁D₁中，M为A₁D₁中点，过A₁C₁且与CD₁平行的平面交平面C₁CM于直线l,则直线l与AB所成角的余弦值是（　　）

  A． 3 2

  B． 2 2

  C． 6 + 2 4

  D． 6 3
  组卷：80引用：3难度：0.6

  解析

• 7．奔驰定理：已知O是△ABC内的一点，△BOC，△AOC，△AOB的面积分别为S_A，S_B，S_C，则S_A•

  OA

  +S_B•

  OB

  +S_C•

  OC

  =

  0

  ．“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车的logo很相似，故形象地称其为“奔驰定理”．设O为三角形ABC内一点，且满足

  OA

  +2

  OB

  +3

  OC

  =3

  AB

  +2

  BC

  +

  CA

  ，则

  S

  △

  AOB

  S

  △

  ABC

  =（　　）

  A． 2 5

  B． 1 2

  C． 1 6

  D． 1 3
  组卷：624引用：7难度：0.6

  解析

四、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）

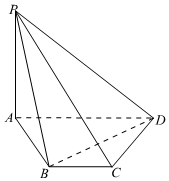• 21．如图，在四棱锥P-ABCD中，AD=2，AB=BC=CD=1，BC∥AD，∠PAD=90°，∠PBA为锐角，平面PBA⊥平面PBD．
  （1）证明：PA⊥平面ABCD；
  （2）若AD与平面PBD所成角的正弦值为

  2

  4

  ，求二面角P-BD-C的余弦值．
  组卷：523引用：5难度：0.5

  解析

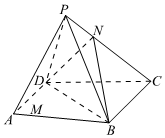• 22．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，AD=CD=3，BC=4，△PBC为正三角形，点M，N分别在线段AD和PC上，且

  DM

  AM

  =

  CN

  PN

  =

  2

  ．设二面角P-AD-B为θ，且

  cosθ

  =

  1

  3

  ．
  （1）求证：PM∥平面BDN；
  （2）求直线PM与平面PBC所成角的正弦值；
  （3）求三棱锥P-ABN的体积．
  组卷：322引用：2难度：0.6

  解析