2023-2024学年陕西省西安市蓝田县田家炳中学高二（上）月考数学试卷（9月份）

一、单选题（8小题，共40分）

• 1．已知

  a

  =

  （

  -

  1

  ，

  3

  ，-

  2

  ）

  ，

  b

  =

  （

  1

  ，-

  1

  ，

  m

  ）

  ，且

  a

  •

  b

  =-2，则m=（　　）

  A．-1

  B．1

  C．-2

  D．2
  组卷：125引用：5难度：0.9

  解析

• 2．已知直线ax+by-1=0在y轴上的截距为-1，且它的倾斜角为

  π

  4

  ，则a-b=（　　）

  A．0

  B．1

  C．-2

  D．2
  组卷：50引用：5难度：0.8

  解析

• 3．已知常数a,b∈R，且a,b不全为零，若直线ax+by=1与圆C：x²+y²=1相交，则点P（a,b）与圆C的位置关系是（　　）

  A．点在圆内

  B．点在圆上

  C．点在圆外

  D．随a、b取值的变化而变化
  组卷：45引用：2难度：0.6

  解析

• 4．

  （

  x

  -

  a

  ）

  2

  +

  （

  y

  -

  b

  ）

  2

  可以转化为平面上M（x,y）点与点N（a,b）之间的距离．结合上述观点，可得

  f

  （

  x

  ）

  =

  x

  2

  +

  8

  x

  +

  20

  +

  x

  2

  +

  4

  x

  +

  20

  的最小值为（　　）

  A． 29

  B． 2 10

  C． 31

  D． 2 + 13
  组卷：39引用：1难度：0.8

  解析

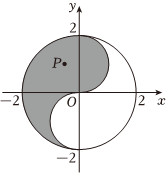• 5．“太极图”因其形状如对称的阴阳两鱼互抱在一起，故也被称为“阴阳鱼太极图”．如图是放在平面直角坐标系中的“太极图”，图中曲线为圆或半圆，已知点P（x,y）是阴影部分（包括边界）的动点，则

  y

  x

  -

  2

  的最小值为（　　）

  A． - 2 3

  B． - 3 2

  C． - 4 3

  D．-1
  组卷：685引用：42难度：0.7

  解析

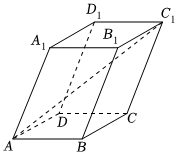• 6．如图，平行六面体ABCD-A₁B₁C₁D₁的底面ABCD是矩形，其中AB=2，AD=4，AA₁=3，且∠A₁AD=∠A₁AB=60°，则线段AC₁的长为（　　）

  A．9

  B． 29

  C． 47

  D． 4 3
  组卷：213引用：9难度：0.5

  解析

• 7．已知正三棱柱ABC-A₁B₁C₁的侧棱长为3，底面边长为2，则直线AB₁与侧面ACC₁A₁所成角的正弦值等于（　　）

  A． 39 13

  B． 130 13

  C． 2 2

  D． 3 2
  组卷：148引用：2难度：0.6

  解析

四、解答题（6小题，共70分）

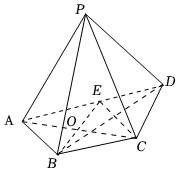• 21．如图所示，在四棱锥P-ABCD中，PA⊥平面PCD，底面ABCD满足AD∥BC，AP=AB=BC=

  1

  2

  AD=4，∠ABC=90°，E为AD的中点，AC与BE的交点为O．
  （1）设H是线段BE上的动点，证明：三棱锥H-PCD的体积是定值；
  （2）（文科生做）求四棱锥P-ABCD的体积．
  （理科生做）求直线BC与平面PBD所成角的余弦值．
  组卷：37引用：3难度：0.6

  解析

• 22．已知圆C过

  A

  （

  1

  ，-

  7

  ）

  ，

  B

  （

  6

  ，

  2

  3

  ）

  ，且圆心C在x轴上．
  （1）求圆C的标准方程；
  （2）若直线l过点D（2，10），且被圆C截得的弦长为

  4

  3

  ，求直线l的方程；
  （3）过点C且不与x轴重合的直线与圆C相交于M，N，O为坐标原点，直线OM，ON分别与直线x=8相交于P，Q，记△OMN，△OPQ面积为S₁，S₂，求

  S

  1

  S

  2

  的最大值．
  组卷：297引用：6难度：0.5

  解析