2021-2022学年山西省太原外国语学校九年级（上）月考数学试卷（12月份）

一．选择题（共10小题）

• 1．下列关系式中，表示y是x的反比例函数的是（　　）

  A． y = 1 x 2

  B． y = x 3

  C． y = 2 x + 1

  D． y = 3 x
  组卷：57引用：3难度：0.6

  解析

• 2．如图所示的礼品盒的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：4引用：1难度：0.8

  解析

• 3．已知△ABC∽△DEF，相似比为1：2，且△DEF的面积为12，则△ABC的面积为（　　）

  A．48

  B．12

  C．6

  D．3
  组卷：16引用：1难度：0.5

  解析

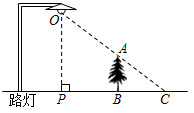• 4．如图，小树AB在路灯O的照射下形成投影BC．若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m.则路灯的高度OP为（　　）

  A．3m

  B．4m

  C．4.5m

  D．5m
  组卷：2260引用：27难度：0.5

  解析

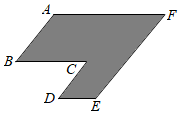• 5．如图，阴影部分是一个菱形剪去一个平行四边形后所剩下的，要想知道阴影部分的周长，需要测量线段（　　）的长度．

  A．AB与BC

  B．AB与DE

  C．AF

  D．AB
  组卷：241引用：5难度：0.7

  解析

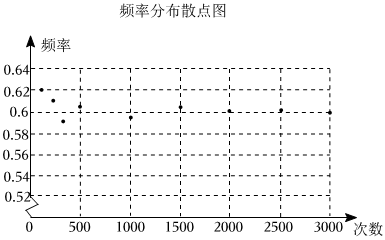
• 6．数学兴趣小组在一次用频率估计概率的实验中统计了某一结果出现的频率，绘制了如图所示的频率分布散点图，则符合这一结果的实验可能是（　　）
  

  A．抛掷一枚硬币，正面向上的概率

  B．抛掷一枚骰子，朝上一面的点数为3的倍数的概率

  C．从装有3个红球、2个黄球袋子中，随机摸出一球为红球的概率

  D．一副去掉大小王的普通扑克牌洗匀后，从中任抽一张，牌的花色是红桃的概率
  组卷：68引用：2难度：0.7

  解析

• 7．《九章算术》是我国古代数学的经典著作，它的出现标志着中国古代数学形成了完整的体系，其“勾股”章中记载了一个数学问题：“今有户高多于广六尺，两隅相去适一丈，问户高、广各几何？”译文为：“已知有一扇矩形门的高比宽多6尺，门的对角线长为1丈（1丈=10尺），那么门的高和宽各是多少？”如果设门的宽为x尺，则可列方程为（　　）

  A．x2+（x+6）2=102	B．x2+（x+6）2=12
  C．x2+（x-6）2=102	D．x2+（x-6）2=12
  组卷：445引用：14难度：0.6

  解析

• 8．如图，矩形ABCD的对角线AC、BD相交于点O，过点O的直线EF分别交AD、BC于点E、F．若AB=6，BC=10则图中阴影部分的面积为（　　）

  A．24

  B．30

  C．48

  D．60
  组卷：13引用：2难度：0.5

  解析

三、解答题（本大题共8个小题，共75分）

• 23．感知：
  （1）数学课上，老师给出了一个模型：如图1，∠BAD=∠ACB=∠AED=90°，由∠1+∠2+∠BAD=180°，∠2+∠D+∠AED=180°，可得∠1=∠D；又因为∠ACB=∠AED=90°，可得△ABC∽△DAE，进而得到

  BC

  AC

  =

  ．我们把这个数学模型称为“一线三等角”模型．
  应用：
  （2）实战组受此模型的启发，将三等角变为非直角，如图2，在△ABC中，点D在边BC上，并且DA=DE，∠B=∠ADE=∠C．若BC=a,AB=b,求CE的长度（用含a,b的代数式表示）．
  拓展：
  （3）创新组突发奇想，将此模型迁移到平行四边形中，如图3，在▱ABCD中，E为边BC上的一点，F为边AB上的一点．若∠DEF=∠B．求证：AB•FE=BE•DE．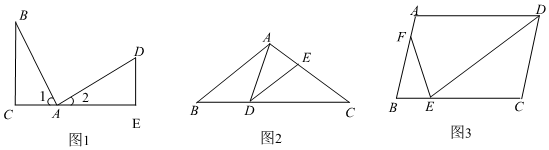
  
  组卷：771引用：4难度：0.2

  解析

• 24．综合与探究
  如图，直线y=-x+m与反比例函数

  y

  =

  k

  x

  的图象相交于点A（-2，n），与x轴交于点B（2，0）．
  （1）求m和k的值；
  （2）点C在x轴的负半轴上，直线AC与反比例函数

  y

  =

  k

  x

  的图象交于点D，若D是AC的中点，求△AOC的面积；
  （3）若点P与点O关于直线AB对称，连接AP．
  ①求点P的坐标；
  ②若点M在反比例函数

  y

  =

  k

  x

  的图象上，点N在x轴上，以点A，P，M，N为顶点的四边形能否为平行四边形？若能，直接写出点M的坐标；若不能，请说明理由．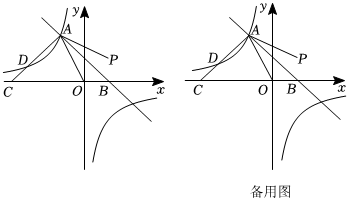
  
  组卷：85引用：1难度：0.1

  解析