当前位置：试卷中心 > 试卷详情

2023-2024学年北京市朝阳区和平街一中九年级（上）调研数学试卷（9月份）

发布：2024/9/8 1:0:8

一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个。

1．下列方程中是一元二次方程的是（　　）
A．xy+2=1 B．
1
x
2
-
x
=
1
C．x（x-3）=0 D．x³+2x=0
组卷：116引用：3难度：0.5
解析
2．用配方法解一元二次方程x²-8x+2=0，此方程可化为的正确形式是（　　）
A．（x-4）²=14 B．（x-4）²=18 C．（x+4）²=14 D．（x+4）²=18
组卷：1873引用：25难度：0.4
解析
3．二次函数y=x²的图象经过的象限是（　　）
A．第一、二象限 B．第一、三象限
C．第二、四象限 D．第三、四象限
组卷：650引用：8难度：0.8
解析
4．对于y=3（x-1）²+2的性质，下列叙述正确的是（　　）
A．顶点坐标为（-1，2）
B．当x=1时，y随x增大而减小
C．当x=1时，y有最大值2
D．对称轴为直线x=1
组卷：354引用：3难度：0.6
解析
5．一元二次方程4x²+1=-4x的根的情况是（　　）
A．只有一个实数根 B．有两个不相等的实数根
C．有两个相等的实数根 D．没有实数根
组卷：502引用：8难度：0.6
解析
6．已知x₁和x₂是方程x²-x-1=0的两个根，则x₁²+x₁x₂+x₂²的值是（　　）
A．1 B．2 C．3 D．-1
组卷：53引用：5难度：0.9
解析
7．已知点A（x₁，y₁），B（x₂，y₂）是抛物线y=（x-1）²-2上两点，若x₁＜x₂＜0，则y₁与y₂的大小关系是（　　）
A．y₁＜y₂ B．y₁＞y₂
C．y₁=y₂ D．以上都有可能
组卷：228引用：4难度：0.5
解析
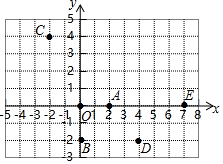8．如图，在平面直角坐标系xOy中，有五个点A（2，0），B（0，-2），C（-2，4），D（4，-2），E（7，0），将二次函数y=a（x-2）²+m（m≠0）的图象记为W．下列判断中：
①A一定不在W上；
②点B，C，D可以同时在W上；
③点C，E不可能同时在W上．
所有正确结论的序号是（　　）
A．①②③ B．①② C．①③ D．②③
组卷：241引用：2难度：0.6
解析

二、填空题（本题共16分，每小题2分）

9．请写出一个开口向下，对称轴为直线x=3的抛物线的解析式
．
组卷：257引用：4难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共68分，第17-18题，每小题6分，第19-20题，每小题6分，第21-22题，每小题6分，第23-26题，每小题6分，第27，28题，每小题6分)

27．在△ABC中，∠ACB=90°，D为△ABC内一点，连接BD，DC，延长DC到点E，使得CE=DC．
（1）如图1，延长BC到点F，使得CF=BC，连接AF，EF．若AF⊥EF，求证：BD⊥AF；
（2）连接AE，交BD的延长线于点H，连接CH，依题意补全图2．若AB²=AE²+BD²，用等式表示线段CD与CH的数量关系，并证明．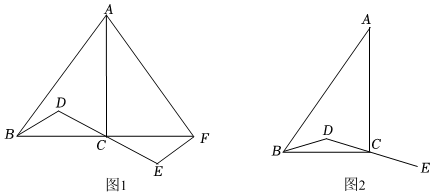
组卷：5412引用：22难度：0.6
解析
28．在平面直角坐标系xOy中，对于已知的点P，Q，过点P分别作x轴和y轴的垂线l₁，l₂，记点Q到直线l₁的距离为d₁，点Q到直线l₂的距离为d₂，若d₁≥d₂，则点Q到点P的“特征距离”为d₁，若d₁＜d₂，则点Q到点P的“特征距离”为d₂．
（1）已知点A（1，2）
①点B（-2，3）到点A的“特征距离”为
；
②点C在函数y=x²的图象上，若点C到点A的“特征距离”为1，则点C的坐标为
；
（2）已知点P（3，4），点E（a,0），F（0，b）为平面内的动点，其中a,b均为非负数，且满足EF=2．以EF为边作正方形EFGH（E、F、G、H按顺时针方向排列），记线段GH上一动点Q到点P的“特征距离”为t,直接写出t的最大值和最小值，以及相应的H点的坐标．
组卷：279引用：2难度：0.1
解析