2023-2024学年重庆市缙云教育联盟高二(上)质检数学试卷(9月份)
发布:2024/8/31 3:0:11
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
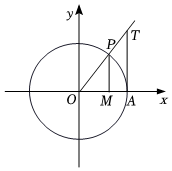 1.如图,已知点A是单位圆与x轴的交点,角α的终边与单位圆的交点为P,PM⊥x轴于M,过点A作单位圆的切线交角α的终边于T,则角α的正弦线、余弦线、正切线分别是( )组卷:95引用:4难度:0.7
1.如图,已知点A是单位圆与x轴的交点,角α的终边与单位圆的交点为P,PM⊥x轴于M,过点A作单位圆的切线交角α的终边于T,则角α的正弦线、余弦线、正切线分别是( )组卷:95引用:4难度:0.7 -
2.已知角α的终边经过点(-1,6),则cosα=( )
组卷:247引用:3难度:0.8 -
3.函数f(x)=2sin2(
+x)-π4cos2x的最大值为( )3组卷:54引用:1难度:0.9 -
4.下列角中与
终边相同的是( )-5π4组卷:397引用:1难度:0.8 -
5.若sin(
)=π4-x,则cos(-15)的值为( )5π4+x组卷:73引用:5难度:0.9 -
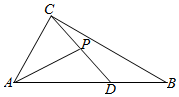 6.如图,在△ABC中,,∠BAC=π3,P为CD上一点,且满足AD=2DB,若AP=mAC+13AB,则AB•AC=4的最小值是( )|AP|组卷:466引用:5难度:0.6
6.如图,在△ABC中,,∠BAC=π3,P为CD上一点,且满足AD=2DB,若AP=mAC+13AB,则AB•AC=4的最小值是( )|AP|组卷:466引用:5难度:0.6 -
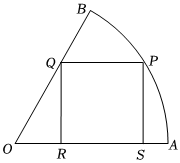 7.如图,已知扇形AOB的半径为2,其圆心角为,四边形PQRS是该扇形的内接矩形,则该矩形面积的最大值为( )π4组卷:239引用:5难度:0.7
7.如图,已知扇形AOB的半径为2,其圆心角为,四边形PQRS是该扇形的内接矩形,则该矩形面积的最大值为( )π4组卷:239引用:5难度:0.7
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
-
21.已知sinx+2cosx=0.
(1)求tanx的值;
(2)求的值.3sinx-cosx3sinx+cosx组卷:46引用:2难度:0.7 -
22.在△ABC中,点D,E,F分别在边AB,BC,AC上,且
=3AB,DB=3AF,3FC,P是CD,EF的交点.设BE=2EC,AB=a.AC=b
(1)用,a表示b,CD;EF
(2)求的值.|CP||PD|组卷:66引用:2难度:0.5


