2021-2022学年四川省资阳外国语实验学校高二（下）期中数学试卷（文科）

一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知复数z=2-3i,则

  （

  z

  +

  1

  ）

  i

  =（　　）

  A．3-i

  B．-3+3i

  C．3+i

  D．-3+i
  组卷：19引用：3难度：0.8

  解析

• 2．f（x）=sinx,则f'（1）与[f（1）]'分别为（　　）

  A．cos1与cos1

  B．cos1与sin1

  C．cos1与0

  D．0与cos1
  组卷：114引用：3难度：0.8

  解析

• 3．设抛物线y²=8x上一点P到y轴的距离是4，则点P到该抛物线焦点的距离是（　　）

  A．4

  B．6

  C．8

  D．12
  组卷：1581引用：59难度：0.9

  解析

• 4．曲线

  x

  2

  25

  -

  y

  2

  9

  =1与曲线

  x

  2

  25

  +

  k

  -

  y

  2

  9

  -

  k

  =1（-25＜k＜9）的（　　）

  A．实轴长相等

  B．虚轴长相等

  C．离心率相等

  D．焦距相等
  组卷：98引用：2难度：0.7

  解析

• 5．将曲线y=sin2x按照伸缩变换

  x ′ = 2 x

  y ′ = 3 y

  后得到的曲线方程为（　　）

  A．y=3sinx

  B．y=3sin2x

  C．y=3sin 1 2 x

  D．y= 1 3 sin2x
  组卷：620引用：10难度：0.9

  解析

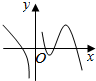• 6．设f（x）在定义域内可导，其图象如图所示，则导函数f′（x）的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：1621引用：26难度：0.9

  解析

• 7．为了研究某种细菌在特定环境下随时间变化的繁殖情况，得到的实验数据如表，并由此计算得到回归直线方程

  ̂

  y

  =

  0

  .

  85

  x

  -

  0

  .

  25

  ，后来工作人员不慎将下表中的实验数据c丢失．
  

  天数x/天	3	4	5	6	7
  繁殖个数y/千个	c	3	4	4.5	6

  则上表中丢失的实验数据c的值为（　　）

  A．1

  B．1.5

  C．2

  D．2.5
  组卷：145引用：3难度：0.8

  解析

三、解答题：本大题共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．已知

  F

  （

  1

  2

  ，

  0

  ）

  为抛物线y²=2px（p＞0）的焦点，点N（x₀，y₀）（y₀＞0）为其上一点，M与N关于x轴对称，直线l与抛物线交于异于M、N的A、B两点，

  |

  NF

  |

  =

  5

  2

  ，K_NA•K_NB=-2．
  （Ⅰ）求抛物线的标准方程和N点的坐标；
  （Ⅱ）判断是否存在这样的直线l,使得△MAB的面积最小．若存在，求出直线l的方程和△MAB面积的最小值；若不存在，请说明理由．
  组卷：136引用：2难度：0.5

  解析

• 22．已知函数f（x）=lnx.
  （1）过原点作f（x）的切线l,求l的方程；
  （2）令g（x）=

  f

  （

  x

  ）

  x

  ，求g（x）≥a在[

  e

  ，e⁴]恒成立，求a的取值范围．
  组卷：57引用：2难度：0.5

  解析