当前位置：试卷中心 > 试卷详情

2022-2023学年广东省梅州市丰顺县砂田学校九年级（上）月考数学试卷（9月份）

发布：2024/8/24 15:0:10

一、选择题（共10题，共30分）

1．用配方法解下列方程，其中应在方程左、右两边同时加上4的是（　　）
A．x²-2x=5 B．2x²-4x=5 C．x²+4x=5 D．4x²+4x=5
组卷：106引用：12难度：0.9
解析
2．一元二次方程2x²-3x+1=0根的情况是（　　）
A．有两个不相等的实数根 B．有两个相等的实数根
C．只有一个实数根 D．没有实数根
组卷：1419引用：46难度：0.7
解析
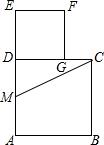3．如图，在边长为2的正方形ABCD中，M为边AD的中点，延长MD至点E，使ME=MC，以DE为边作正方形DEFG，点G在边CD上，则DG的长为（　　）
A．
3
-
1
B．
3
-
5
C．
5
+
1
D．
5
-
1
组卷：3017引用：108难度：0.9
解析
4．如图，已知直线l₁∥l₂∥l₃∥l₄，相邻两条平行直线间的距离都是1，如果正方形ABCD的四个顶点分别在四条直线上，则正方形ABCD的面积为（　　）
A．4 B．5 C．9 D．
24
5
组卷：876引用：4难度：0.7
解析
5．如图，将矩形纸片ABCD按如下步骤操作，将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，恰好满足MP=MN=NF，则下列结论中，正确的有（　　）个．①∠MNF=∠PQF；②△EMF≌△GNF；③∠MNF=60°；④AD=3
3
AB．
A．4 B．3 C．2 D．1
组卷：194引用：2难度：0.5
解析
6．如图，正方形ABCD中，对角线AC、BD交于点O，∠BAC的平分线交BD于E，交BC于F，BH⊥AF于H，交AC于G，交CD于P，连接GE、GF，以下结论：①△OAE≌△OBG；②四边形BEGF是菱形；③BE=CG；④
PG
AE
=
2
-1；⑤S_△PBC：S_△AFC=1：2，其中正确的有（　　）个．
A．2 B．3 C．4 D．5
组卷：951引用：7难度：0.4
解析
7．下列性质中，矩形具有而菱形不一定具有的是（　　）
A．对角线相等 B．对角线互相平分
C．对角线互相垂直 D．邻边相等
组卷：236引用：8难度：0.6
解析
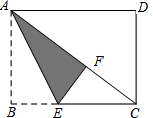8．如图，在矩形纸片ABCD中，已知AD=8，折叠纸片，使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为（　　）
A．3 B．4 C．5 D．6
组卷：3162引用：32难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共8题，共62分）

24．类比学习：
有这样一个命题：设x、y、z都是小于1的正数，求证：x（1-y）+y（1-z）+z（1-x）＜1．
小明同学是这样证明的：如图，作边长为1的正三角形ABC，并分别在其边上截取AD=x,BE=z,CF=y,设△ADF、△CEF和△BDE的面积分别为S₁、S₂、S₃，
则
S
1
=
1
2
x
（
1
-
y
）
sin
60
°
，
S
2
=
1
2
y
（
1
-
z
）
sin
60
°
，
S
3
=
1
2
z
（
1
-
x
）
sin
60
°
．
由S₁+S₂+S₃＜S_△ABC，得
1
2
x
（
1
-
y
）
sin
60
°
+
1
2
y
（
1
-
z
）
sin
60
°
+
1
2
z
（
1
-
x
）
sin
60
°
＜
3
4
．
所以x（1-y）+y（1-z）+z（1-x）＜1．
类比实践：
已知正数a、b、c、d,x、y、z、t满足a+x=b+y=c+z=d+t=k.
求证：ay+bz+ct+dx＜2k²．
组卷：74引用：4难度：0.5
解析
25．在菱形ABCD中，∠ABC=60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE，点E的位置随着点P的位置变化而变化．

（1）如图1，当点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系是
，CE与AD的位置关系是
；
（2）当点E在菱形ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由（选择图2，图3中的一种情况予以证明或说理）；
（3）如图4，当点P在线段BD的延长线上时，连接BE，若AB=2
3
，BE=2
19
，求四边形ADPE的面积．
组卷：5340引用：25难度：0.1
解析