2022-2023学年北京五中高二（下）期末数学试卷

一、单选题（每小题4分，共40分）

• 1．已知集合A={x|1＜x＜3}，B={x|x≤2}，那么集合A∩B等于（　　）

  A．{x|1＜x＜2}

  B．{x|2＜x＜3}

  C．{x|1＜x≤2}

  D．{x|2≤x＜3}
  组卷：23引用：4难度：0.9

  解析

• 2．若复数z满足i•z=3-4i,则|z|=（　　）

  A． 10

  B．5

  C．7

  D．25
  组卷：114引用：3难度：0.8

  解析

• 3．（x-2y）⁴的展开式中含x²y²的项的系数为（　　）

  A．24

  B．-24

  C．6

  D．-6
  组卷：157引用：3难度：0.8

  解析

• 4．关于向量

  a

  ，

  b

  ，

  c

  ，下列命题中正确的是（　　）

  A．若 | a | = | b | ，则 a = b	B．若 a = - b ，则 a ∥ b
  C．若 a ∥ b ， b ∥ c ，则 a ∥ c	D．若 | a | ＞ | b | ，则 a ＞ b
  组卷：389引用：6难度：0.8

  解析

• 5．布达佩斯的伊帕姆维泽蒂博物馆收藏的达•芬奇方砖，在正六边形上画了具有视觉效果的正方体图案（如图1），把三片这样的达•芬奇方砖形成图2的组合，这个组合表达了图3所示的几何体．如图3中每个正方体的棱长为1，则点A到平面QGC的距离是（　　）

  A． 1 4

  B． 1 2

  C． 2 2

  D． 3 2
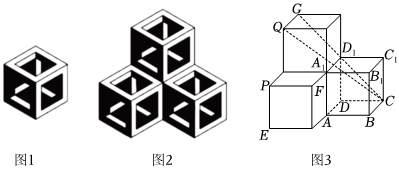  组卷：185引用：10难度：0.5

  解析

• 6．点F是抛物线x²=8y的焦点，A为双曲线C：

  x

  2

  8

  -

  y

  2

  b

  =

  1

  的左顶点，直线AF平行于双曲线C的一条渐近线，则实数b的值为（　　）

  A．2

  B．4

  C．8

  D．16
  组卷：613引用：7难度：0.5

  解析

• 7．在△ABC中，角A，B，C所对的边分别为a,b,c,∠A=60°，且△ABC的面积为

  3

  ，若b+c=6，则a=（　　）

  A． 2 6

  B．5

  C． 30

  D． 2 7
  组卷：306引用：7难度：0.6

  解析

三、解答原（第16-19、21题14分，第20题15分）

• 20．已知函数f（x）=e^x，g（x）=ln（x+a）（a∈R）．
  （1）求曲线y=f（x）在点（1，f（1））处的切线方程；
  （2）设φ（x）=f（x）g（x），请判断φ（x）是否存在极值？若存在，求出极值；若不存在，说明理由；
  （3）当a=0时，若对于任意s＞t＞0，不等式

  g

  （

  s

  ）

  -

  g

  （

  t

  ）

  ＞

  k

  （

  1

  f

  （

  s

  ）

  -

  1

  f

  （

  t

  ）

  ）

  恒成立，求k的取值范围．
  组卷：689引用：4难度：0.3

  解析

• 21．已知各项均为整数的数列A_N：a₁，a₂，…，a_N（N≥3，N∈N*）满足a₁a_N＜0，且对任意i=2，3，…，N，都有|a_i-a_i-1|≤1．记S（A_N）=a₁+a₂+…+a_N．
  （Ⅰ）若a₁=3，写出一个符合要求的A₆；
  （Ⅱ）证明：数列A_N中存在a_k使得a_k=0；
  （Ⅲ）若S（A_N）是N的整数倍，证明：数列A_N中存在a_r，使得S（A_N）=N•a_r．
  组卷：224引用：6难度：0.2

  解析