当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省无锡市市北高级中学高二（上）期初数学试卷

发布：2024/8/11 12:0:1

一、单项选择题（本大题共8小题，每小题5分，共计40分，在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案填涂在答题卡相应位置上）

1．若复数z满足i•z=3-4i,则|z|=（　　）
A．1 B．5 C．7 D．25
组卷：2528引用：28难度：0.8
解析
2．设α，β为两个不同的平面，m,n为两条不同的直线，下列命题正确的是（　　）
A．若m∥n,n⊂α，则m∥α
B．若m∥α，n∥β，m∥n,则α∥β
C．若m⊥β，n∥β，则m⊥n
D．若α⊥β，α∩β=m,n⊥m,则n⊥α
组卷：217引用：12难度：0.6
解析
3．若圆锥的母线长为
2
3
，侧面展开图的面积为6π，则该圆锥的体积是（　　）
A．
3
π
B．3π C．
3
3
π
D．9π
组卷：645引用：13难度：0.8
解析
4．若
a
，
b
，
c
是空间三个单位向量，
a
，
b
夹角为60°，
a
⊥
c
，
|
a
+
2
b
+
3
c
|
=
10
，则
〈
b
，
c
〉
=（　　）
A．30° B．60° C．90° D．120°
组卷：27引用：2难度：0.7
解析
5．三星堆古遗址作为“长江文明之源“，被誉为人类最伟大的考古发现之一.3号坑发现的神树纹玉琮，为今人研究古蜀社会中神树的意义提供了重要依据．玉琮是古人用于祭祀的礼器，有学者认为其外方内圆的构造，契合了古代“天圆地方”观念，是天地合一的体现，如图，假定某玉琮形状对称，由一个空心圆柱及正方体构成，且圆柱的外侧面内切于正方体的侧面，圆柱的高为12cm,圆柱底面外圆周和正方体的各个顶点均在球O上，则球O的表面积为（　　）
A．72πcm² B．162πcm² C．216πcm² D．288πcm²
组卷：302引用：7难度：0.7
解析
6．P是△ABC所在平面上一点，满足|
PB
-
PC
|-|
PB
+
PC
-
2
PA
|=0，则△ABC的形状是（　　）
A．等腰直角三角形 B．直角三角形
C．等腰三角形 D．等边三角形
组卷：1105引用：17难度：0.7
解析
7．在△ABC中，AB=2AC=2，P，Q为线段BC上的点，且
BP
=
PQ
=
QC
．若
AP
•
AQ
=
5
9
，则∠BAC=（　　）
A．150° B．120° C．60° D．30°
组卷：171引用：6难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）

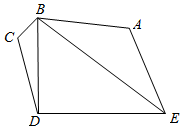21．杭州市为迎接2022的亚运会，规划公路自行车比赛赛道，该赛道的平面示意图为如图的五边形ABCDE，运动员的公路自行车比赛中如出现故障，可以从本队的器材车、公共器材车上或收容车上获得帮助．比赛期间，修理或更换车轮或赛车等，也可在固定修车点上进行．还需要运送一些补给物品，例如食物、饮料、工具和配件．所以项目设计需要预留出BD，BE为赛道内的两条服务通道（不考虑宽度），ED，DC，CB，BA，AE为赛道，∠BCD=∠BAE=
2
π
3
，∠CBD=
π
4
，CD=2
6
km,DE=8km.
（1）从以下两个条件中任选一个条件，求服务通道BE的长度；
①∠CDE=
7
π
12
；②cos∠DBE=
3
5
．
（2）在（1）的条件下，应该如何设计，才能使折线赛道BAE最长（即BA+AE最大），最长值为多少？
组卷：354引用：9难度：0.5
解析
22．已知向量
a
=（cos
3
x
2
，sin
3
x
2
），
b
=（cos
x
2
，-sin
x
2
），函数f（x）=
a
•
b
-m|
a
+
b
|+1，x∈[-
π
6
，
π
4
]，x∈R．
（1）若|
a
+
b
|=
3
，求实数x的值；
（2）若f（x）的最小值为-1，求实数m的值；
（3）是否存在实数m,使函数
g
（
x
）
=
f
（
x
）
+
24
49
m
2
，
x
∈
[
-
π
6
，
π
4
]
有四个不同的零点？若存在，求出m的取值范围；若不存在，请说明理由．
组卷：269引用：3难度：0.2
解析