2022-2023学年江苏省泰州市高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项符合题目要求。

• 1．已知向量

  m

  =

  （

  1

  ，

  2

  ，

  3

  ）

  与

  n

  =

  （

  2

  ，

  x

  ,

  6

  ）

  垂直，则实数x的值为（　　）

  A．-10

  B．-4

  C．4

  D．10
  组卷：14引用：1难度：0.7

  解析

• 2．书架上有3本不同的数学书，4本不同的物理书，图书管理员从中任取2本，则不同的取法种数为（　　）

  A．7

  B．12

  C．21

  D．42
  组卷：53引用：3难度：0.8

  解析

• 3．口袋中有2个黑球，2个红球和1个白球，这些球除颜色外完全相同．任取两球，用随机变量X表示取到的黑球数，则P（X=2）的值为（　　）

  A． 1 5

  B． 1 10

  C． 3 10

  D． 3 5
  组卷：45引用：1难度：0.7

  解析

• 4．某中学通过问卷调查的形式统计了该校1000名学生完成作业所需的时间，发现这些学生每天完成作业所需的时间（单位：小时）近似地服从正态分布

  N

  （

  1

  ，

  1

  16

  ）

  ．则这1000名学生中每天完成作业所需的时间不少于1.5小时的人数大约为（　　）
  附：随机变量ξ服从正态分布N（μ，σ²），则P（μ-σ＜ξ＜μ+σ）≈0.683，P（μ-2σ＜ξ＜μ+2σ）≈0.954．

  A．23

  B．46

  C．158

  D．317
  组卷：63引用：1难度：0.7

  解析

• 5．在（x+1）（x+2）（x+3）（x+4）的展开式中，含x³项的系数为（　　）

  A．50

  B．35

  C．24

  D．10
  组卷：263引用：5难度：0.7

  解析

• 6．已知x,y的取值如下表所示，从散点图分析可知y与x线性相关，如果线性回归方程为

  ̂

  y

  =

  0

  .

  95

  x

  +

  2

  .

  5

  ，则下列说法不正确的是（　　）
  

  x	0	1	2	3	4
  y	2.3	4.3	4.4	4.8	m

  A．m的值为6.2

  B．回归直线必过点（2，4.4）

  C．样本点（4，m）处的残差为0.1

  D．将此图表中的点（2，4.4）去掉后，样本相关系数r不变
  组卷：63引用：1难度：0.7

  解析

• 7．已知三棱柱ABC-A₁B₁C₁的侧棱长为2，底面ABC是边长为2的正三角形，∠A₁AB=∠A₁AC=60°，若B₁C和BC₁相交于点M．则

  |

  AM

  |

  =（　　）

  A． 3

  B．2

  C． 5

  D． 6
  组卷：57引用：5难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．

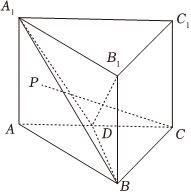• 21．如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，AA₁=1，D为AC的中点．请从条件①、②、③中选择合适的两个作为已知，并解答下面的问题：
  （1）求二面角A₁-BD-B₁所成角的正弦值；
  （2）点P是矩形AA₁B₁B（包含边界）内任一点，且

  CP

  =

  2

  ，求CP与平面B₁BD所成角的正弦值的取值范围．
  条件①：平面A₁BC的面积为

  6

  2

  ；
  条件②：C₁D⊥A₁B；条件③：B₁点到平面A₁BC的距离为

  6

  3

  ．
  组卷：64引用：1难度：0.6

  解析

• 22．某软件科技公司近8年的年利润y与投入的年研发经费x（单位：千万元）如下表所示．
  

  x	3	4	5	6	6	7	8	9
  y	y1	y2	y3	y4	y5	y6	y7	y8

  （1）根据散点图可以认为x与y之间存在线性相关关系，且相关系数

  r

  =

  83

  84

  ，请用最小二乘法求出线性回归方程

  ̂

  y

  =

  ̂

  b

  x

  +

  ̂

  a

  （

  ̂

  a

  ，

  ̂

  b

  用分数表示）；
  （2）某配件加工厂加工的单个零件尺寸与标准件尺寸的误差

  ε

  ～

  N

  （

  0

  ，

  6

  c

  +

  1

  ）

  ，其中c为单个零件的加工成本（单位：元），且

  P

  （

  |

  ε

  |

  ＜

  1

  2

  ）

  =

  0

  .

  954

  ．引进该公司最新研发的某工业软件后，加工的单个零件尺寸与标准件尺寸的误差

  ε

  ～

  N

  （

  0

  ，

  11

  2

  c

  +

  2

  ）

  ．若保持零件加工质量不变（即误差的概率分布不变），则单个零件加工的成本下降了多少元？
  附：（1）参考数据：

  8

  ∑

  i

  =

  1

  y

  i

  2

  =

  3452

  ，

  8

  ∑

  i

  =

  1

  （

  y

  i

  -

  y

  ）

  2

  =

  252

  ．
  （2）参考公式：

  r

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  n

  ∑

  i

  =

  1

  （

  y

  i

  -

  y

  ）

  2

  ，

  ̂

  b

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  ，

  ̂

  a

  =

  y

  -

  ̂

  b

  x

  ．
  （3）若随机变量ξ服从正态分布N（μ，σ²），则P（μ-σ＜ξ＜μ+σ）≈0.683，P（μ-2σ＜ξ＜μ+2σ）≈0.954．
  组卷：81引用：3难度：0.6

  解析