2023-2024学年江苏省无锡市江阴市南菁高级中学高二（上）月考数学试卷（10月份）

一、单选题

• 1．已知等比数列{a_n}的前2项和为2，前4项和为8，则它的前6项和为（　　）

  A．12

  B．22

  C．26

  D．32
  组卷：103引用：3难度：0.7

  解析

• 2．过点P（-1，3）且垂直于直线x-2y+3=0的直线方程为（　　）

  A．2x+y-1=0

  B．2x+y-5=0

  C．x+2y-5=0

  D．x-2y+7=0
  组卷：2781引用：179难度：0.9

  解析

• 3．已知数列{a_n}的前n项和为S_n，且

  a

  1

  =

  -

  10

  ，

  a

  n

  +

  1

  =

  a

  n

  +

  3

  （

  n

  ∈

  N

  *

  ）

  ，则S_n取最小值时，n的值是（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：90引用：15难度：0.7

  解析

• 4．已知A（0，1），B（1，0），点C在圆（x+1）²+（y+2）²=18上，若三角形ABC的面积为1，则点C的个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：23引用：3难度：0.5

  解析

• 5．已知{a_n}为递增数列，前n项和

  S

  n

  =

  2

  n

  +

  2

  n

  2

  +

  λ

  ，则实数λ的取值范围是（　　）

  A．（-∞，2]

  B．（-∞，2）

  C．（-∞，4]

  D．（-∞，4）
  组卷：153引用：2难度：0.6

  解析

• 6．圆

  C

  1

  ：

  x

  2

  +

  y

  2

  +

  2

  ax

  +

  a

  2

  -

  1

  =

  0

  和圆

  C

  2

  ：

  x

  2

  +

  y

  2

  -

  4

  by

  -

  1

  +

  4

  b

  2

  =

  0

  有三条公切线，若a∈R，b∈R，ab≠0，则

  4

  a

  2

  +

  1

  b

  2

  的最小值为（　　）

  A．4

  B．6

  C．8

  D．10
  组卷：95引用：2难度：0.5

  解析

• 7．已知圆C：x²+y²=8，MN为圆C的动弦，且满足MN=4，G为弦MN的中点．两动点P，Q在直线l：y=x-4上，且PQ=4，MN运动时，∠PGQ始终为锐角，则线段PQ中点的横坐标取值范围是（　　）

  A．（-∞，0）∪（4，+∞）	B．（-∞，0）∪（8，+∞）
  C．（0，4）	D．（0，8）
  组卷：219引用：7难度：0.6

  解析

四、解答题

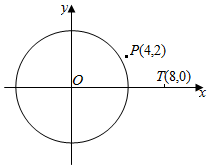• 21．已知直角坐标系xOy中，圆O：x²+y²=16．
  ①过点P（4，2）作圆O的切线m,求m的方程；
  ②直线l：y=kx+b与圆O交于点M，N两点，已知T（8，0），若x轴平分∠MTN，证明：不论k取何值，直线l与x轴的交点为定点，并求出此定点坐标．
  组卷：147引用：2难度：0.6

  解析

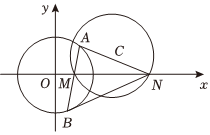• 22．圆C：x²-（1+a）x+y²-ay+a=0．
  （1）若圆C与y轴相切，求圆C的方程；
  （2）已知a＞1，圆C与x轴相交于两点M，N（点M在点N的左侧）．过点M任作一条直线与圆O：x²+y²=9相交于两点A，B．问：是否存在实数a,使得∠ANM=∠BNM．若存在，求出实数a,若不存在，请说明理由．
  组卷：156引用：4难度：0.5

  解析