2023-2024学年云南师大附中高二(上)月考数学试卷(10月份)
发布:2024/9/6 6:0:10
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的)
-
1.已知集合M={x|x+2≥0},N={x|x-1<0}.则M∩N=( )
组卷:2628引用:19难度:0.9 -
2.
=( )5(1+i3)(2+i)(2-i)组卷:256引用:7难度:0.8 -
3.若
=(-1,2,3),AB=(1,-1,-5),则BC=( )|AC|组卷:642引用:16难度:0.8 -
4.一组数据4.3,6.5,7.8,6.2,9.6,15.9,7.6,8.1,10,12.3,11,3,则它们的75%分位数是( )
组卷:153引用:4难度:0.7 -
5.已知角α的终边上有一点P(1,3),则
的值为( )cos(3π2-α)+2cos(-π+α)组卷:575引用:5难度:0.7 -
6.在三棱柱ABC-A1B1C1中,
,若点D为B1C1的中点,则AB=a,AC=b,AA1=c=( )CD组卷:328引用:6难度:0.7 -
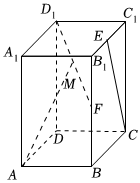 7.已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,点E,F分别是B1C1和BB1的中点,M是线段D1F的中点,则直线AM和CE所成角的余弦值为( )组卷:122引用:6难度:0.7
7.已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,点E,F分别是B1C1和BB1的中点,M是线段D1F的中点,则直线AM和CE所成角的余弦值为( )组卷:122引用:6难度:0.7
四、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
-
21.已知a∈R,函数
.f(x)=log2(x2-3x+a)
(1)若函数f(x)的图象经过点(3,1),求不等式f(x)<1的解集;
(2)设a>2,若对任意t∈[3,4],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.组卷:89引用:3难度:0.5 -
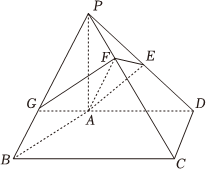 22.如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.过点A作四棱锥P-ABCD的截面AEFG,分别交PD,PC,PB于点E,F,G,且PG:PB=2:3,.PF=λPC
22.如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.过点A作四棱锥P-ABCD的截面AEFG,分别交PD,PC,PB于点E,F,G,且PG:PB=2:3,.PF=λPC
(1)若E为PD的中点,求实数λ的值;
(2)若,求平面AGFE与平面ABCD所成角的正弦值.λ=23组卷:134引用:5难度:0.4


