2022-2023学年江西省九江市彭泽第二高级中学高一(下)期中数学试卷
发布:2024/5/24 8:0:9
一、单选题(每题5分,共40分)
-
1.已知复数
,则z=1-i1+i的虚部为( )z(2+3i)组卷:25引用:2难度:0.8 -
2.设x∈R,则“|x-1|<2”是“x2<x”的( )
组卷:482引用:7难度:0.8 -
3.下列说法正确的是( )
组卷:140引用:6难度:0.9 -
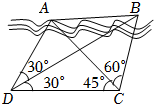 4.如图,为了测量河对岸A,B两点间的距离,在河的这边测定CD=1km,∠ADB=∠CDB=30°,∠DCA=45°,∠ACB=60°,则AB两点距离是( )组卷:183引用:3难度:0.6
4.如图,为了测量河对岸A,B两点间的距离,在河的这边测定CD=1km,∠ADB=∠CDB=30°,∠DCA=45°,∠ACB=60°,则AB两点距离是( )组卷:183引用:3难度:0.6 -
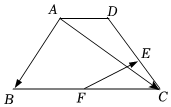 5.如图所示,等腰梯形ABCD中,AB=BC=CD=3AD,点E为线段CD上靠近C的三等分点,点F为线段BC的中点,则=( )FE组卷:217引用:6难度:0.7
5.如图所示,等腰梯形ABCD中,AB=BC=CD=3AD,点E为线段CD上靠近C的三等分点,点F为线段BC的中点,则=( )FE组卷:217引用:6难度:0.7 -
6.在△ABC中,角A,B,C的对边分别是a,b,c,已知b=c=3,3acosA-ccosB=bcosC,则a=( )
组卷:250引用:2难度:0.7 -
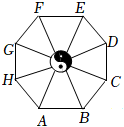 7.《易经》是阐述天地世间关于万象变化的古老经典,如图所示的是《易经》中记载的几何图形——八卦图.图中正八边形代表八卦,中间的圆代表阴阳太极图,其余八块面积相等的图形代表八卦田.已知正八边形ABCDEFGH的边长为,点P是正八边形ABCDEFGH边上的一点,则22的最小值是( )AP•AB组卷:69引用:3难度:0.5
7.《易经》是阐述天地世间关于万象变化的古老经典,如图所示的是《易经》中记载的几何图形——八卦图.图中正八边形代表八卦,中间的圆代表阴阳太极图,其余八块面积相等的图形代表八卦田.已知正八边形ABCDEFGH的边长为,点P是正八边形ABCDEFGH边上的一点,则22的最小值是( )AP•AB组卷:69引用:3难度:0.5
四、解答题(共70分)
-
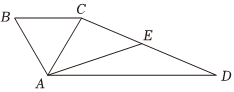 21.如图,在四边形ABCD中,BC∥AD,BC=1,AD=3,△ABC为等边三角形,E是CD的中点.设,AB=a.AD=b
21.如图,在四边形ABCD中,BC∥AD,BC=1,AD=3,△ABC为等边三角形,E是CD的中点.设,AB=a.AD=b
(1)用,a表示b,AC;AE
(2)求∠BAE的余弦值.组卷:270引用:8难度:0.5 -
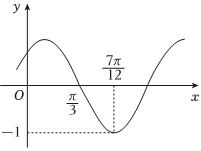 22.已知函数的部分图像如图所示.f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)
22.已知函数的部分图像如图所示.f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)
(1)求函数y=f(x)的解析式;
(2)将y=f(x)的图像上所有点的横坐标缩短到原来的,纵坐标不变,再向右平移12个单位长度得到y=g(x)的图像,求函数g(x)的单调递增区间;π6
(3)在第(2)问的前提下,对于任意,是否总存在实数x1∈[-π3,π3],使得f(x1)+g(x2)=m成立?若存在,求出实数m的值或取值范围;若不存在,说明理由.x2∈[-π6,π6]组卷:335引用:8难度:0.5


