2023-2024学年江苏省连云港市灌南县教育联盟校九年级（上）质检数学试卷（A卷）

一、选择题（本大题共8小题，每小题3分，共24分.在每小题所给出的四个选项

• 1．下列方程是一元二次方程的是（　　）

  A．x2-2=0

  B．2x-1=0

  C． 3 x 2 = 2

  D．x3-1=0
  组卷：41引用：1难度：0.9

  解析

• 2．已知⊙O的半径为3，若点A在⊙O外，则OA的长度可能是（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：39引用：3难度：0.7

  解析

• 3．方程x²-3x-1=0的根的情况是（　　）

  A．两个不相等的实数根	B．两个相等的实数根
  C．两个实数根	D．无法确定实根的个数
  组卷：53引用：1难度：0.7

  解析

• 4．用配方法解方程x²+4x+1=0时，配方结果正确的是（　　）

  A．（x-2）2=5

  B．（x-2）2=3

  C．（x+2）2=5

  D．（x+2）2=3
  组卷：2671引用：86难度：0.7

  解析

• 5．如图，在⊙O中，

  ˆ

  AB

  =

  ˆ

  AC

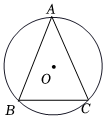  ，∠B=70°，则∠A的度数为（　　）

  A．20°

  B．40°

  C．70°

  D．110°
  组卷：197引用：7难度：0.7

  解析

• 6．某超市一月份的营业额为200万元，一月、二月、三月的营业额共1000万元，如果平均每月增长率为x,则由题意列方程应为（　　）

  A．200+200（1+x）+200（1+x）2=1000

  B．200（1+x）2=1000

  C．200+200•3•x=1000

  D．200+200•2•x=1000
  组卷：496引用：9难度：0.6

  解析

• 7．AB、CD是⊙O中的两条弦，若AB=2CD，则

  ˆ

  AB

  与2

  ˆ

  CD

  的大小关系是（　　）

  A． ˆ AB ＞2 ˆ CD

  B． ˆ AB ＜2 ˆ CD

  C． ˆ AB =2 ˆ CD

  D．不能确定
  组卷：403引用：1难度：0.7

  解析

• 8．已知y₁和y₂均是以x为自变量的函数，当x=m时，函数值分别是M₁和M₂，若存在实数m,使得M₁+M₂=0，则称函数y₁和y₂具有性质P．以下函数y₁和y₂具有性质P的是（　　）

  A． y 1 = x 2 + 2 x 和y2=-x-1	B． y 1 = x 2 + 2 x 和y2=-x+1
  C． y 1 = - 1 x 和y2=-x-1	D． y 1 = - 1 x 和y2=-x+1
  组卷：590引用：8难度：0.6

  解析

三、解答题（本大题共8小题，共96分.请在答题卡上指定区域内作答.解答时写出必要的文字说明、证明过程或演算步骤，)

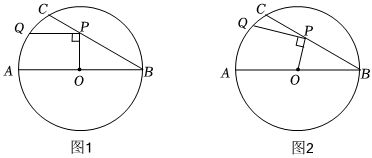• 25．在⊙O中，直径AB=10，BC是弦，∠ABC=30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．
  （1）如图1，当PQ∥AB时，求PQ的长度；
  （2）如图2，当点P在BC上移动时，求PQ长的最大值．
  组卷：408引用：1难度：0.5

  解析

• 26．我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用，例如：试求二次三项式x²+4x+5最小值．
  解：x²+4x+5=x²+4x+4+1=（x+2）²+1，
  ∵（x+2）²≥0，（x+2）²+1≥1，
  ∴x²+4x+5≥1，即x²+4x+5的最小值是1．
  试利用“配方法”解决下列问题：
  （1）已知y=-x²-8x+14求y的最大（或最小）值．
  （2）比较代数式2x²+3x-5与3x²-x+1的大小，并说明理由．
  （3）知识迁移：
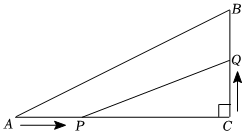
  如图，在Rt△ABC中，∠C=90°，AC=8cm,BC=6cm,点P在AC边上以2cm/s的速度从点A向C移动，点Q在CB边上以1cm/s的速度从点C向点B移动．若点P，Q同时出发，且当一点移动到终点时，另一点也随之停止，设四边形APQB的面积为S cm²运动时间为t秒，求S的最小值．
  组卷：284引用：1难度：0.2

  解析