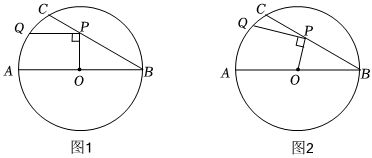
在⊙O中，直径AB=10，BC是弦，∠ABC=30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．
（1）如图1，当PQ∥AB时，求PQ的长度；
（2）如图2，当点P在BC上移动时，求PQ长的最大值．
【答案】（1）；
（2）．
5
6
3
（2）
5
3
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/7 1:0:8组卷：408引用：1难度：0.5
相似题
-
1．Rt△ABC中，∠ABC=90°，以AB为直径作⊙O交AC边于点D，E是边BC的中点，连接DE，OD．
（Ⅰ）如图①，求∠ODE的大小；
（Ⅱ）如图②，连接OC交DE于点F，若OF=CF，求∠A的大小．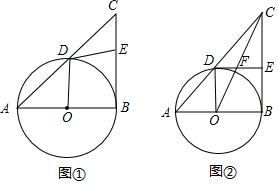
发布：2025/6/18 2:30:1组卷：2269引用：2难度：0.1 -
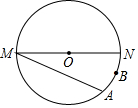2．如图，MN是⊙O的直径，MN=4，点A在⊙O上，∠AMN=30°，B为弧AN的中点，P是直径MN上一动点，则PA+PB的最小值为．发布：2025/6/17 21:0:1组卷：1009引用：5难度：0.5 -
3．如图，四边形ABCD为正方形，⊙O过正方形的顶点A和对角线的交点P，分别交AB、AD于点F、E．
（1）求证：DE=AF；
（2）若⊙O的半径为，AB=32，求2+1的值．AEED发布：2025/6/17 22:0:1组卷：2956引用：5难度：0.3
