我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用，例如：试求二次三项式x2+4x+5最小值．
解：x2+4x+5=x2+4x+4+1=（x+2）2+1，
∵（x+2）2≥0，（x+2）2+1≥1，
∴x2+4x+5≥1，即x2+4x+5的最小值是1．
试利用“配方法”解决下列问题：
（1）已知y=-x2-8x+14求y的最大（或最小）值．
（2）比较代数式2x2+3x-5与3x2-x+1的大小，并说明理由．
（3）知识迁移：
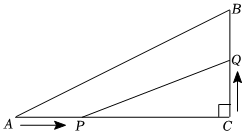
如图，在Rt△ABC中，∠C=90°，AC=8cm,BC=6cm,点P在AC边上以2cm/s的速度从点A向C移动，点Q在CB边上以1cm/s的速度从点C向点B移动．若点P，Q同时出发，且当一点移动到终点时，另一点也随之停止，设四边形APQB的面积为S cm2运动时间为t秒，求S的最小值．
【答案】（1）30；（2）2x2+3x-5＜3x2-x+1；（3）20．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/7 1:0:8组卷：284引用：1难度：0.2
