当前位置：试卷中心 > 试卷详情

2022-2023学年陕西省西安市高新一中高一（下）期末数学试卷

发布：2024/6/12 8:0:8

1．已知向量
a
=
（
1
，
2
）
，
b
=
（
3
，
x
）
，
a
与
b
共线，则
|
b
|
=（　　）
A．
3
5
2
B．
3
5
C．
2
5
D．5
组卷：62引用：1难度：0.8
解析
2．已知P（-1，2）为抛物线C：y²=-2px（p＞0）上一点，则C的焦点坐标为（　　）
A．
（
-
1
4
，
0
）
B．
（
-
1
2
，
0
）
C．
（
-
3
2
，
0
）
D．（-1，0）
组卷：94引用：1难度：0.8
解析
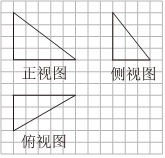3．如图是某三棱锥的三视图，已知网格纸的小正方形边长是1，则这个三棱锥中最长棱的长为（　　）
A．5 B．
34
C．
41
D．7
组卷：112引用：6难度：0.7
解析
4．已知椭圆
x
2
10
-
m
+
y
2
m
-
2
=1长轴在x轴上，若焦距为4，则m等于（　　）
A．4 B．5 C．7 D．8
组卷：4439引用：13难度：0.9
解析
5．已知圆锥的母线长为2，侧面积为
2
3
π
，则此圆锥的轴截面的面积等于（　　）
A．2 B．
2
C．3 D．
3
组卷：114引用：2难度：0.5
解析
6．在△ABC中，角A，B，C的对边分别为a,b,c,且ccosA=b,则△ABC是（　　）
A．直角三角形 B．锐角三角形
C．等边三角形 D．A=30°的三角形
组卷：42引用：2难度：0.7
解析
7．过点（0，-2）与圆x²+y²-4x-1=0相切的两条直线的夹角为α，则cosα（　　）
A．
1
4
B．
15
4
C．
-
1
4
D．
10
4
组卷：365引用：6难度：0.7
解析

21．已知圆C经过点E（0，6），F（4，4），且圆心在直线l：2x-5y+13=0上．
（1）求圆C的方程．
（2）直线y=kx+3与圆C交于A，B两点，问：在直线y=3上是否存在定点N；使得k_AN+k_BN=0（k_AN、k_BN分别为直线AN，BN的斜率）恒成立？若存在，请求出点N的坐标；若不存在，请说明理由．
组卷：454引用：4难度：0.5
解析
22．已知椭圆
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
过点A（-2，-1），长轴长为
4
2
．
（1）求椭圆C的方程及其焦距；
（2）直线l：y=kx+m与椭圆C交于不同的两点M，N，直线AM，AN分别与直线x=-4交于点P，Q，O为坐标原点且|OP|=|OQ|，求证：直线l过定点，并求出定点坐标．
组卷：496引用：5难度：0.6
解析