2023-2024学年湖南省长沙市雨花区雅礼实验中学九年级(上)第一次月考数学试卷
发布:2024/9/22 5:0:8
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1.下列环保标志图案既是轴对称图形,又是中心对称图形的是( )
组卷:397引用:15难度:0.8 -
2.人体内一种细胞的直径约为0.00000156m,数据0.00000156用科学记数法表示为( )
组卷:779引用:24难度:0.9 -
3.已知⊙O的半径为4cm,当线段OA=4cm时,则点A在( )
组卷:50引用:1难度:0.7 -
4.抛物线y=-x2+4x+1的对称轴是( )
组卷:182引用:2难度:0.6 -
5.如图,用直角曲尺检查半圆形的工件是否合格,运用到的道理是( )
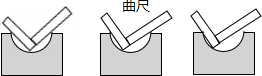 组卷:183引用:4难度:0.9
组卷:183引用:4难度:0.9 -
6.将抛物线y=2x2向左平移4个单位长度,再向上平移1个单位长度得到的抛物线的解析式为( )
组卷:695引用:7难度:0.7 -
7.一个矩形的长比宽多3cm,面积是4cm2,则这个矩形的长为( )
组卷:39引用:1难度:0.7 -
 8.△AOB绕点O逆时针旋转65°后得到△COD,若∠AOB=30°,则∠BOC的度数是( )组卷:551引用:15难度:0.8
8.△AOB绕点O逆时针旋转65°后得到△COD,若∠AOB=30°,则∠BOC的度数是( )组卷:551引用:15难度:0.8
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答写出必要的文字说明、证明过程或演算步骤)
-
24.我们不妨约定:若将函数C1的图象沿某一点旋转180度,与函数C2的图象重合,则称函数C1与函数C2关于这个点互为“中心对称函数”,这个点叫做函数C1与函数C2的“对称中心”,求函数的“中心对称函数”的方法多样,例如:求函数C1:y=x的关于(1,0)的中心对称函数,可以在函数C1上取(0,0)和(1,1),两个点关于(1,0)中心对称点分别是(2,0)和(1,-1),这样我们就可以得到函数y=x关于(1,0)中心对称函数y=x-2.
(1)求函数y=x+1关于(0,0)的中心对称函数;
(2)已知函数C1:y=2x+b,若函数C1关于(0,-b)的中心对称函数C2的图象与函数y=-bx+2的图象的交点是整数点(横、纵坐标都为整数的点称为整数点),求正整数b的值;
(3)已知函数(a,b,c是常数,且a≠0),若函数C1关于(0,0)的中心对称函数C2满足下列两个条件:①a+b+c=0,②(2c+b-a)(2c+b+3a)<0,求函数C2截x轴得到的线段长度的取值范围.C1:y=-ax2+2bx-c组卷:324引用:1难度:0.5 -
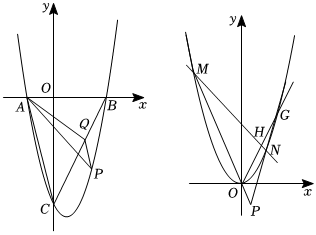 25.抛物线交x轴于A,B两点(A在B的左边),交y轴于点C.C1:y=x2-2x-8
25.抛物线交x轴于A,B两点(A在B的左边),交y轴于点C.C1:y=x2-2x-8
(1)求出A,B,C三点的坐标;
(2)已知点Q是线段BC上的动点,过点Q作PQ∥AC交抛物线的第四象限部分于点P,连接PA,PB,如图①,记△PAQ与△PBQ的面积分别为S1,S2,设S=S1+S2,当S最大时,求点P的坐标;
(3)将抛物线C1平移得到抛物线C2,其顶点为原点,如图②,直线y=2x与抛物线交于O,G两点,过OG的中点作直线MN(异于直线OG)交抛物线C2于M,N两点,直线MO与直线GN交于点P.问点P是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.组卷:439引用:2难度:0.1


