当前位置：试卷中心 > 试卷详情

2023-2024学年天津市和平区九年级（上）期中数学试卷

发布：2024/9/30 11:0:2

一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，

1．我国古代数学的许多创新与发明都曾在世界上有重要影响．下列图形“杨辉三角”“中国七巧板”“刘徽割圆术”“赵爽弦图”中，中心对称图形是（　　）
A． B． C． D．
组卷：1155引用：46难度：0.8
解析
2．若α，β是一元二次方程x²-3x-4=0的两个根，则α+β的值为（　　）
A．-4 B．4 C．-3 D．3
组卷：1033引用：10难度：0.8
解析
3．二次函数y=-5（x+2）²-6的开口方向、对称轴和顶点坐标分别为（　　）
A．向下、直线x=2、（2，6）
B．向下、直线x=-2、（-2，-6）
C．向下、直线x=-2、（-2，6）
D．向上、直线x=2、（2，-6）
组卷：281引用：7难度：0.5
解析
4．已知⊙O的半径为2，
OA
=
5
，则点A和⊙O的位置关系是（　　）
A．点A在圆上 B．点A在圆外 C．点A在圆内 D．不确定
组卷：338引用：4难度：0.5
解析
5．抛物线
y
=
-
1
2
x
2
向左平移1个单位，再向下平移1个单位后的抛物线解析式是（　　）
A．
y
=
-
1
2
（
x
+
1
）
2
+
1
B．
y
=
-
1
2
（
x
+
1
）
2
-
1
C．
y
=
-
1
2
（
x
-
1
）
2
+
1
D．
y
=
-
1
2
（
x
-
1
）
2
-
1
组卷：1072引用：10难度：0.8
解析
6．用配方法解一元二次方程时，首先把x²+6x-5=0化成（x+a）²=b（a、b为常数）的形式，则a+b的值为（　　）
A．8 B．11 C．14 D．17
组卷：207引用：4难度：0.5
解析
7．如图，要设计一幅宽20cm,长30cm的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2：3．如果要使彩条所占面积是图案面积的三分之一，应如何设计彩条的宽度？
若设每个横彩条的宽度为2x cm,则每个竖彩条的宽度为3x cm,则根据题意，列方程为（　　）
A．
（
20
-
4
x
）
（
30
-
6
x
）
=
1
3
×
20
×
30
B．
（
20
-
4
x
）
（
30
-
6
x
）
=
（
1
-
1
3
）
×
20
×
30
C．
（
20
-
6
x
）
（
30
-
4
x
）
=
1
3
×
20
×
30
D．
（
20
-
6
x
）
（
30
-
4
x
）
=
（
1
-
1
3
）
×
20
×
30
组卷：201引用：1难度：0.8
解析
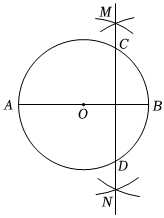8．如图，AB是⊙O的直径，分别以点O和点B为圆心，大于
1
2
OB
的长为半径作弧（弧所在圆的半径都相等），两弧相交于M，N两点，直线MN与⊙O相交于C，D两点，若AB=4，则CD的长为（　　）
A．
4
3
B．4 C．
2
3
D．
3
组卷：520引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，共66分.解答应写出文字说明、演算步骤或推理过程）

25．已知矩形ABCD，AB=3，BC=5，将矩形ABCD绕A顺时针旋转α（0°＜α＜180°），得到矩形AEFG，点B的对应点是点E，点C的对应点是点F，点D的对应点是点G．

（1）如图①；当α=90°时，连接CF，求CF的长；
（2）如图②，当边EF'经过点D时，延长FE交BC于点P，求EP的长；
（3）连接CF，点M是CF的中点，连接BM，在旋转过程中，线段BM的最大值
．
组卷：338引用：4难度：0.2
解析
26．已知抛物线y=ax²+bx+c（a,b,c是常数，a≠0）的顶点为M（1，-4），与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C．
（Ⅰ）若点C（0，-3），求点A和点B的坐标；
（Ⅱ）将点A绕点B逆时针方向旋转90°，点A的对应点为A₁，若A，A₁两点关于点M中心对称，求点A₁的坐标和抛物线解析式；
（Ⅲ）在（Ⅰ）的条件下，点P为直线BC下方抛物线上的一个动点，过点P作PD∥x轴，与BC相交于点D，过点P作PE∥y轴，与x轴相交于点E，求PD+PE的最大值及此时点P的坐标．
组卷：278引用：1难度：0.3
解析