2022-2023学年福建省宁德一中高二（下）月考数学试卷（5月份）

一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）

• 1．某物体做直线运动，其运动规律是

  s

  =

  t

  2

  +

  1

  t

  （t单位是秒，s的单位是米），则它在t=1的瞬时速度为（　　）

  A．0.5

  B．1

  C．2

  D．3
  组卷：54引用：2难度：0.8

  解析

• 2．已知

  a

  =（-2，-3，1），

  b

  =（2，0，4），

  c

  =（-4，-6，2），则下列结论正确的是（　　）

  A． a ∥ c ， b ∥ c

  B． a ∥ b ， a ⊥ c

  C． a ∥ c ， a ⊥ b

  D．以上都不对
  组卷：319引用：20难度：0.9

  解析

• 3．函数y=x+sin|x|，x∈[-π，π]的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：746引用：41难度：0.6

  解析

• 4．在n次独立重复试验（伯努利试验）中，若每次试验中事件A发生的概率为p,则事件A发生的次数X服从二项分布B（n,p），事实上，在伯努利试验中，另一个随机变量的实际应用也很广泛，即事件A首次发生时试验进行的次数Y，显然P（Y=k）=p（1-p）^k-1，k=1，2，3，…，我们称Y服从“几何分布”，经计算得

  EY

  =

  1

  p

  ．据此，若随机变量X服从二项分布

  B

  （

  n

  ,

  1

  6

  ）

  时，且相应的“几何分布”的数学期望E（Y）＜E（X），则n的最小值为（　　）

  A．6

  B．18

  C．36

  D．37
  组卷：95引用：4难度：0.7

  解析

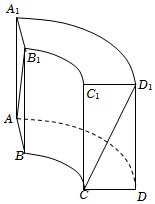• 5．在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体，该几何体的上、下底面平行，且均为扇环形（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池，它的高为2，AA₁，BB₁，CC₁，DD₁均与曲池的底面垂直，底面扇环对应的两个圆的半径分别为1和2，对应的圆心角为90°，则图中异面直线AB₁与CD₁所成角的余弦值为（　　）

  A． 4 5

  B． 3 5

  C． 3 4

  D． 2 3
  组卷：231引用：12难度：0.6

  解析

• 6．已知函数f（x）=（x-1）e^x-mx在区间[2，4]上存在单调减区间，则实数m的取值范围为（　　）

  A．（2e2，+∞）

  B．（-∞，e）

  C．（0，2e2）

  D．（0，e）
  组卷：221引用：6难度：0.6

  解析

• 7．已知正方体ABCD-A₁B₁C₁D₁的棱长为4，球O是正方体的内切球，MN是球O的直径，点G是正方体表面上的一个动点，则

  GM

  •

  GN

  的取值范围为（　　）

  A．[0，4]

  B．[0，8]

  C．[1，11]

  D．[3，12]
  组卷：163引用：4难度：0.6

  解析

四、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算过程．）

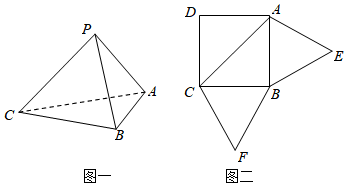• 21．已知三棱锥P-ABC（如图一）的平面展开图（如图二）中，四边形ABCD为边长等于

  2

  的正方形，△ABE和△BCF均为正三角形，在三棱锥P-ABC中：
  （1）证明：平面PAC⊥平面ABC；
  （2）若点M在棱PA上运动，当直线BM与平面PAC所成的角最大时，求二面角M-BC-A的余弦值．
  组卷：209引用：8难度：0.4

  解析

• 22．已知函数f（x）=lnx+x,g（x）=x+e^x+a（a∈R），其中e为自然对数的底数．
  （1）求曲线y=f（x）在点（1，f（1））处的切线方程；
  （2）当a=-2时，有

  τ

  （

  x

  ）

  =

  x 2 - 8 x + 15 ， 2 ≤ x ＜ 6

  9 - x , x ≥ 6

  ，求证：对∀x∈[2，+∞），有g（x）≥τ（x）；
  （3）若f（x₁）-g（x₂）=a,且

  x

  1

  x

  2

  ≥

  1

  ，求实数a的取值范围．
  组卷：13引用：3难度：0.3

  解析