北师大新版八年级上册《第1章 勾股定理》2023年单元测试卷

一、选择题

• 1．以直角三角形的两直角边为边长所作正方形的面积分别是36与64，则斜边长为（　　）

  A．5

  B．10

  C．12

  D．100
  组卷：99引用：3难度：0.5

  解析

• 2．若一直角三角形的两边长分别为12和5，则第三边长的平方是（　　）

  A．169

  B．169或119

  C．13或15

  D．15
  组卷：645引用：8难度：0.7

  解析

• 3．下面说法正确的是（　　）

  A．在Rt△ABC中，a2+b2=c2

  B．在Rt△ABC中，a=3，b=4，那么c=5

  C．直角三角形两直角边都是5，那么斜边长为10

  D．直角三角形中，斜边最长
  组卷：428引用：5难度：0.7

  解析

• 4．如图，要从电线杆离地面3.6m处向地面拉一条长为4.5m的钢缆，则地面钢缆固定点A到电线杆底部点B的距离是（　　）

  A．2m

  B．2.2m

  C．2.4m

  D．2.7m
  组卷：88引用：2难度：0.7

  解析

• 5．如图，等腰三角形ABC底边上的高AD为4cm,腰长为5cm,周长为16cm,则△ABC的面积是（　　）

  A．14cm2

  B．13cm2

  C．12cm2

  D．8cm2
  组卷：149引用：3难度：0.5

  解析

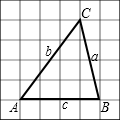• 6．如图，每个小正方形的边长为1，△ABC的三边a,b,c的大小关系式（　　）

  A．a＜c＜b

  B．a＜b＜c

  C．c＜a＜b

  D．c＜b＜a
  组卷：1037引用：36难度：0.9

  解析

• 7．在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a,b,c,若a+b=14cm,c=10cm,则Rt△ABC的面积是（　　）

  A．24cm2

  B．36cm2

  C．48cm2

  D．60cm2
  组卷：410引用：5难度：0.7

  解析

三、解答题

• 22．张老师在一次“探究性学习”课中，设计了如下数表：
  

  n	2	3	4	5	…
  a	22-1	32-1	42-1	52-1	…
  b	4	6	8	10	…
  c	22+1	32+1	42+1	52+1	…

  （1）请你分别观察a,b,c与n之间的关系，并用含自然数n（n＞1）的代数式表示：
  a=

  ，b=

  ，c=

  ；
  （2）猜想：以a,b,c为边的三角形是否为直角三角形并证明你的猜想．
  组卷：2179引用：63难度：0.3

  解析

• 23．如图所示，图（1）是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为a和b.斜边长为c.图（2）是以c为直角边的等腰直角三角形，请你开动脑筋，将它们拼成一个能证明勾股定理的图形．
  （1）在作图区画出拼成的这个图形的示意图，写出它是什么图形．
  （2）用这个图形证明勾股定理．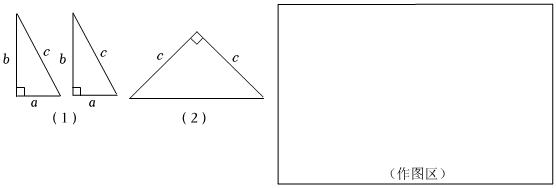
  
  （3）假设现在有一个正方形和若干个全等的直角三角形，且正方形的边长与直角三角形的斜边相等，你能拼出另一种能证明勾股定理的图形吗？请画出拼后的示意图．（无需证明）
  组卷：54引用：2难度：0.6

  解析