2022-2023学年四川省成都七中高二(下)入学数学试卷(理科)
发布:2024/8/9 8:0:9
一、选择题:(本大题共12个小题,每小题5分,共60分,在每小题给出的选项中,只一项是符合要求的。)
-
1.抛物线x2=
y的准线方程是( )14组卷:66引用:6难度:0.9 -
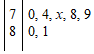 2.在一次数学测验中,统计7名学生的成绩分布茎叶图如图所示,若这7名学生的平均成绩为77分,则x的值为( )组卷:17引用:7难度:0.9
2.在一次数学测验中,统计7名学生的成绩分布茎叶图如图所示,若这7名学生的平均成绩为77分,则x的值为( )组卷:17引用:7难度:0.9 -
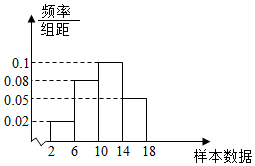 3.容量为100的样本,其数据分布在[2,18],将样本数据分为4组:[2,6),[6,10),[10,14),[14,18],得到频率分布直方图如图所示.则下列说法不正确的是( )组卷:211引用:10难度:0.8
3.容量为100的样本,其数据分布在[2,18],将样本数据分为4组:[2,6),[6,10),[10,14),[14,18],得到频率分布直方图如图所示.则下列说法不正确的是( )组卷:211引用:10难度:0.8 -
4.下列叙述:①某人射击1次,“射中7环”与“射中8环”是互斥事件;
②甲、乙两人各射击1次,“至少有1人射中目标”与“没有人射中目标”是对立事件;
③抛掷一枚硬币,连续出现4次正面向上,则第5次出现反面向上的概率大于;12
④在相同条件下,进行大量重复试验,可以用频率来估计概率;则所有正确结论的序号是( )组卷:198引用:3难度:0.6 -
 5.惊艳全世界的南非双曲线大教堂是由伦敦著名的建筑事务所steynstudio完成的,建筑师的设计灵感源于想法:“你永无止境的爱是多么的珍贵,人们在你雄伟的翅膀下庇护”.若将如图所示的双曲线大教堂外形弧线的一段近似看成双曲线y2-=1(m>0)下支的一部分,且此双曲线的一条渐近线方程为2x-my=0,则此双曲线的离心率为( )x2m组卷:79引用:5难度:0.8
5.惊艳全世界的南非双曲线大教堂是由伦敦著名的建筑事务所steynstudio完成的,建筑师的设计灵感源于想法:“你永无止境的爱是多么的珍贵,人们在你雄伟的翅膀下庇护”.若将如图所示的双曲线大教堂外形弧线的一段近似看成双曲线y2-=1(m>0)下支的一部分,且此双曲线的一条渐近线方程为2x-my=0,则此双曲线的离心率为( )x2m组卷:79引用:5难度:0.8 -
6.在区间[0,π]上随机取一个数θ,使得
成立的概率是( )2≤2sinθ+2cosθ≤2组卷:12引用:2难度:0.6 -
7.若圆O1:x2+y2=1与圆O2:(x-a)2+(y-2a)2=4有公共点,则实数a的取值范围是( )
组卷:160引用:6难度:0.6
三、解答题:(本大题共6个小题,17题10分其余每道小题各12分,共70分,解答时应写出文字说明、证明过程或演算步骤。)
-
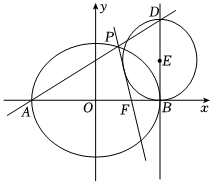 21.已知椭圆的两个焦点与短轴的一个端点恰好围成面积为C:x2a2+y2b2=1(a>b>0)的等边三角形.3
21.已知椭圆的两个焦点与短轴的一个端点恰好围成面积为C:x2a2+y2b2=1(a>b>0)的等边三角形.3
(1)求C的方程;
(2)如图,设C的左,右顶点分别为A,B,右焦点为F,P是C上异于A,B的动点,直线AP与直线x=a交于点D,当点P运动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.组卷:42引用:2难度:0.6 -
22.已知椭圆C:
的左、右焦点分别为F1,F2,离心率为x2a2+y2b2=1(a>b>0),33为C上一点,过点F1且与y轴不垂直的直线l与C交于A,B两点.(3,6)
(1)求C的方程;
(2)在平面内是否存在定点Q,使得为定值?若存在,求出点Q的坐标;若不存在,请说明理由.QA•QB组卷:33引用:4难度:0.5


