2023-2024学年浙江省宁波市北仑中学高二(上)期初数学试卷
发布:2024/8/5 8:0:8
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知
,则z的虚部是( )z=2+i1+i2+i5组卷:35引用:3难度:0.8 -
2.设等比数列{an}的首项为1,公比为q,前n项和为Sn.令bn=Sn+2,若{bn}也是等比数列,则q=( )
组卷:2747引用:2难度:0.8 -
3.下列正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,则能满足AB∥平面MNP的是( )
组卷:215引用:4难度:0.5 -
4.已知一个等比数列的前n项和、前2n项和、前3n项和分别为P、Q、R,则下列等式正确的是( )
组卷:276引用:4难度:0.5 -
5.在锐角△ABC中,角A,B,C的对边分别为a,b,c,若a2=2S+(b-c)2,其中S为△ABC的面积,则sinB的取值范围为( )
组卷:128引用:3难度:0.6 -
6.三棱锥P-ABC中,平面PAB⊥平面ABC,△ABC是边长为2的正三角形,
,则三棱锥P-ABC外接球的表面积为( )PA=PB=3组卷:487引用:7难度:0.5 -
7.若O是△ABC的外心,且
,则sinB+2sinC的最大值是( )AC2AB2•(AB•AO)+AB2AC2•(AC•AO)=52AO2组卷:534引用:3难度:0.3
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.如图,在平行四边形ABCD中,∠ABC=60°,AD=2AB=4,E为AD的中点,以EC为折痕将△CDE折起,使点D到达点P的位置,且PB=
,F,G分别为BC,PE的中点.10
(1)证明:PB∥平面AFG;
(2)若平面PAB与平面PEF的交线为l,求直线l与平面PBC所成角的正弦值.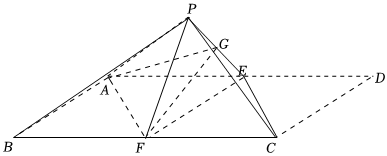 组卷:307引用:5难度:0.3
组卷:307引用:5难度:0.3 -
22.已知数列{an}中a1=1,关于x的函数f(x)=x2-nan+1cosx+(n+1)an有唯一零点,记
.Sn=1an2+1an2+1+1an2+2+…+1(an+1)2-1
(Ⅰ)判断函数f(x)=x2-nan+1cosx+(n+1)an的奇偶性并证明;
(Ⅱ)求an;
(Ⅲ)求证:.2n+1<Sn组卷:41引用:1难度:0.4


