2023-2024学年山东省青岛大学附中八年级（上）期中数学检测试卷

一、选择题（本大题共10小题，共30分）

• 1．下列四组数能作为直角三角形三边长的是（　　）

  A．0.1，0.2，0.3	B．1，1，2
  C．10，24，26	D．32，42，52
  组卷：133引用：4难度：0.7

  解析

• 2．下列各式成立的是（　　）

  A． 1 25 144 =1 5 12	B．（ 3 - 3 ）3=-3
  C． （ - 4 ） 2 =-4	D． 9 =±3
  组卷：300引用：3难度：0.8

  解析

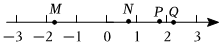• 3．如图，M、N、P、Q是数轴上的点，那么

  5

  在数轴上对应的点可能是（　　）

  A．点M

  B．点N

  C．点P

  D．点Q
  组卷：528引用：9难度：0.7

  解析

• 4．在平面直角坐标系中，第一象限内的点P（a+3，a）到y轴的距离是5，则a的值为（　　）

  A．-8

  B．2或-8

  C．2

  D．8
  组卷：3178引用：11难度：0.7

  解析

• 5．当a＜-1时，代数式

  |

  1

  +

  a

  |

  -

  a

  2

  的值为（　　）

  A．-1

  B．1

  C．2a+1

  D．-1-2a
  组卷：398引用：6难度：0.7

  解析

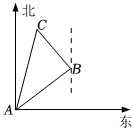• 6．如图，在“庆国庆，手拉手”活动中，某小组从营地A出发，沿北偏东53°方向走了1200m到达B点，然后再沿北偏西37°方向走了500m到达目的地C点，此时A，C两点之间的距离为（　　）

  A．1000m

  B．1100m

  C．1200m

  D．1300m
  组卷：403引用：6难度：0.6

  解析

• 7．已知，点A（-2，y₁），B（-1，y₂），C（1，y₃）都在函数y=-2x+b的图象上，则关于y₁，y₂，y₃的大小关系正确的是（　　）

  A．y3＜y2＜y1

  B．y1＜y2＜y3

  C．y2＜y1＜y3

  D．y3＜y1＜y2
  组卷：123引用：2难度：0.7

  解析

三、解答题（共72分）

• 22．提出问题：已知平面直角坐标系内，任意一点A，到另外一个点B之间的距离是多少？
  问题解决：遇到这种问题，我们可以先从特例入手，最后推理得出结论．
  探究一：点A（1，-1）到B（-1，-1）的距离d₁=

  ；
  探究二：点A（2，-2）到B（-1，-1）的距离d₁=

  ；
  一般规律：（1）如图1，在平面直角坐标系xOy内，已知A（x₁，y₁）、B（x₂，y₂），我们可以表示连接AB，在构造直角三角形，使两条边交于M，且∠M=90°，此时AM=

  ，BM=

  ，AB=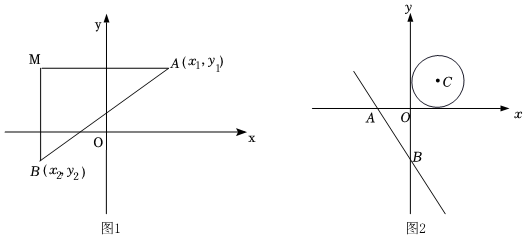

  ．
  
  材料补充：已知点P（x₀，y₀）到直线y=kx+b的距离d₂可用公式d₂=

  |

  k

  x

  0

  -

  y

  0

  +

  b

  |

  1

  +

  k

  2

  计算．
  问题解决：
  （2）已知互相平行的直线y=x-2与y=x+b之间的距离是3

  2

  ，试求b的值．
  拓展延伸：
  拓展一：已知点M（-1，3）与直线y=2x上一点N的距离是3，则△OMN的面积是

  ．
  拓展二：如图2，已知直线y=-

  4

  3

  x

  -

  4

  分别交x,y轴于A，B两点，⊙C是以C（2，2）为圆心，2为半径的圆，P为⊙C上的动点，试求△PAB面积的最大值．
  组卷：387引用：2难度：0.3

  解析

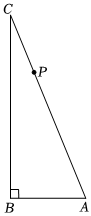• 23．如图，在△ABC中，∠ABC=90°，AC=13，BA=5，点P从点C出发，以每秒3个单位长度的速度沿折线C-A-B运动．设点P的运动时间为t（t＞0）秒．
  （1）BC=

  ．
  （2）求斜边AC上的高线长．
  （3）①当P在AB上时，AP的长为

  ，t的取值范围是

  ．（用含t的代数式表示）
  ②若点P在∠BCA的角平分线上，则t的值为

  ．
  （4）在整个运动过程中，直接写出△PAB是以AB为一腰的等腰三角形时t的值．
  组卷：867引用：2难度：0.5

  解析