提出问题：已知平面直角坐标系内，任意一点A，到另外一个点B之间的距离是多少？
问题解决：遇到这种问题，我们可以先从特例入手，最后推理得出结论．
探究一：点A（1，-1）到B（-1，-1）的距离d1=22；
探究二：点A（2，-2）到B（-1，-1）的距离d1=1010；
一般规律：（1）如图1，在平面直角坐标系xOy内，已知A（x1，y1）、B（x2，y2），我们可以表示连接AB，在构造直角三角形，使两条边交于M，且∠M=90°，此时AM=x1-x2x1-x2，BM=y1-y2y1-y2，AB=（x1-x2）2+（y1-y2）2（x1-x2）2+（y1-y2）2．
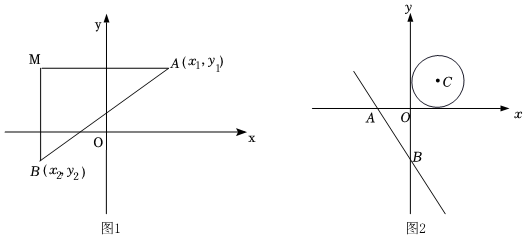
材料补充：已知点P（x0，y0）到直线y=kx+b的距离d2可用公式d2=|kx0-y0+b|1+k2计算．
问题解决：
（2）已知互相平行的直线y=x-2与y=x+b之间的距离是32，试求b的值．
拓展延伸：
拓展一：已知点M（-1，3）与直线y=2x上一点N的距离是3，则△OMN的面积是 52±552±5．
拓展二：如图2，已知直线y=-43x-4分别交x,y轴于A，B两点，⊙C是以C（2，2）为圆心，2为半径的圆，P为⊙C上的动点，试求△PAB面积的最大值．
10
10
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
|
k
x
0
-
y
0
+
b
|
1
+
k
2
2
5
2
±
5
5
2
±
5
4
3
x
-
4
【考点】一次函数综合题．
【答案】2；；x1-x2；y1-y2；；
10
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
5
2
±
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/2 3:0:2组卷：390引用：2难度：0.3
相似题
-
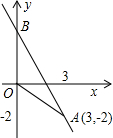1．在直角坐标系中，O是坐标原点，点A（3，-2）在一次函数y=-2x+4图象上，图象与y轴的交点为B，那么△AOB面积为．发布：2025/6/21 1:0:2组卷：608引用：6难度：0.9 -
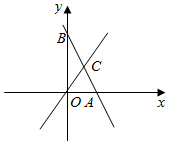2．如图，在平面直角坐标系中，直线y=-2x+4分别交x轴，y轴于A，B两点，与直线OC交于点C．
（1）求点A，B的坐标．
（2）若点C的坐标为（m,2），求线段AC的长．
（3）若P是x轴上一动点，是否存在点P，使△ABP是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．发布：2025/6/21 1:30:2组卷：2149引用：3难度：0.5 -
3．如图，直线
与x轴相交于点A，与直线y=-3x+43相交于点P．y=3x
（1）求点P的坐标．
（2）请判断△OPA的形状并说明理由．
（3）动点E从原点O出发，以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动（E不与点O、A重合），过点E分别作EF⊥x轴于F，EB⊥y轴于B．设运动t秒时，矩形EBOF与△OPA重叠部分的面积为S．求S与t之间的函数关系式．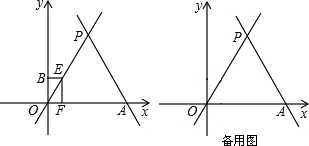
发布：2025/6/20 22:30:2组卷：954引用：7难度：0.3
