2022-2023学年河南省洛阳市栾川第一高级中学高三(下)入学数学试卷
发布:2024/6/6 8:0:9
一、单项选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知复数z满足z(1+i)=2i,则复数
的模是( )z组卷:58引用:4难度:0.8 -
2.已知集合
,则A∩(∁RB)=( )A={x|3x2-5x-2≤0},B={x|y=3x-2}组卷:178引用:2难度:0.8 -
3.已知函数f(x)=lnx-ax2+x有两个不同的零点,则实数a的取值范围是( )
组卷:240引用:2难度:0.6 -
4.已知函数f(x)=2x+5x.若
,a=f(log1312),c=f(60.2),则a,b,c的大小关系为( )b=f(log35)组卷:597引用:3难度:0.8 -
5.若曲线C1:y=x2与曲线C2:y=
(a>0)存在公切线,则实数a的取值范围( )exa组卷:466引用:6难度:0.7 -
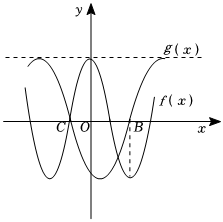 6.函数f(x)=2cos2x和g(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,则不等式的解集是( )g(x)>3组卷:77引用:1难度:0.6
6.函数f(x)=2cos2x和g(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,则不等式的解集是( )g(x)>3组卷:77引用:1难度:0.6 -
7.已知函数
,有如下命题:f(x)=2sinxcosx,g(x)=cos(2x-π3)
①将f(x)的图象向左平移个单位长度可以得到g(x)的图象;π12
②将f(x)的图象向左平移个单位长度可以得到g(x)的图象;π6
③f(x)与g(x)的图象关于直线对称;x=5π12
④f(x)与g(x)的图象关于直线对称.x=5π24
则上述命题中正确的序号是( )组卷:95引用:2难度:0.5
三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知双曲线C:
-x2a2=1经过点(2,3),两条渐近线的夹角为60°,直线l交双曲线于A、B两点.y2b2
(1)求双曲线C的方程;
(2)若l过原点,P为双曲线上异于A,B的一点,且直线PA、PB的斜率kPA,kPB均存在,求证:kPA•kPB为定值;
(3)若l过双曲线的右焦点F1,是否存在x轴上的点M(m,0),使得直线l绕点F1无论怎样转动,都有•MA=0成立?若存在,求出M的坐标;若不存在,请说明理由.MB组卷:625引用:5难度:0.3 -
22.已知函数f(x)=ax2-ex(a∈R).f′(x)是f(x)的导数(e为自然对数的底数).
(Ⅰ)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)若当x≥0时,不等式f(x)≤-x-1恒成立,求实数a的取值范围.组卷:387引用:3难度:0.3


