2022-2023学年山西省晋城一中高一（上）第五次调研数学试卷

一、选择题（本题共8小题，每小题5分，共40分，在下列给出的四个选项中，只有一项是最符合题意的。）

• 1．若集合A={x|x≥0}，且A∩B=B，则集合B可能是（　　）

  A．{x|x≤1}

  B．{1，2}

  C．{-1，0，1 }

  D．R
  组卷：10引用：1难度：0.9

  解析

• 2．已知命题p：∃x₀∈R，（a-1）

  x

  2

  0

  +（a-1）x₀+1≤0，若命题p是假命题，则a的取值范围为（　　）

  A．1≤a≤5

  B．1＜a＜5

  C．1＜a≤5

  D．1≤a＜5
  组卷：81引用：6难度：0.6

  解析

• 3．已知函数f（x）的图象如图1所示，则图2所表示的函数是（　　）

  A．1-f（x）

  B．-f（2-x）

  C．f（-x）-1

  D．1-f（-x）
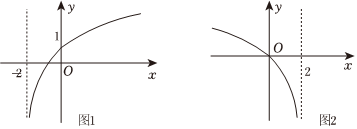  组卷：48引用：2难度：0.8

  解析

• 4．已知关于x的不等式ax²-bx+1＞0的解集为

  （

  -

  ∞

  ，

  2

  m

  ）

  ∪

  （

  m

  ,

  +

  ∞

  ）

  ，其中m＞0，则

  b

  +

  1

  m

  的最小值为（　　）

  A．4

  B． 2 2

  C．2

  D．1
  组卷：181引用：6难度：0.7

  解析

• 5．已知函数f（x）是定义在R上的偶函数，且在[0，+∞）上单调递增，且f（3）=0，则不等式（2x-5）f（x）＜0的解集为（　　）

  A．（-∞，-3）∪（ 5 2 ， 3 ）	B．（3，+∞）
  C．（-∞，3）∪（3，+∞）	D．（-∞，-3）
  组卷：59引用：3难度：0.6

  解析

• 6．为了衡量星星的明暗程度，古希腊天文学家喜帕恰斯在公元前二世纪首先提出了“星等”这个概念．星等的数值越小，星星就越亮，星等的数值越大它的光就越暗．到了1850年，由于光度计在天体光度测量的应用，英国天文学家普森又提出了亮度的概念，天体的明暗程度可以用星等或亮度来描述．两颗星的星等与亮度满足m₁-m₂=2.5（lgE₂-lgE₁），其中星等为m_k的星的亮度为E_k（k=1，2）．已知“心宿二”的星等是1.00，“天津四”的星等是1.25，则“心宿二”的亮度大约是“天津四”的（　　）倍．
  （当|x|较小时，10^x≈1+2.3x+2.7x²）

  A．1.27

  B．1.26

  C．1.23

  D．1.22
  组卷：62引用：6难度：0.8

  解析

• 7．函数f（x）=

  6

  e

  x

  +

  1

  +

  mx

  |

  x

  |

  +

  1

  的最大值为M，最小值为N，则M+N=（　　）

  A．3

  B．4

  C．6

  D．与m值有关
  组卷：212引用：6难度：0.6

  解析

四、解答题：本题共6小题，第17题10分，其余每小题10分，共70分。

• 21．已知函数f（x）=log₂（4^x+1）-kx（其中k∈R），函数

  h

  （

  x

  ）

  =

  lo

  g

  2

  （

  b

  •

  2

  x

  -

  4

  3

  b

  ）

  （其中b∈R）．
  （1）若k=2且函数g（x）=f（x）-a+1存在零点；求a的取值范围；
  （2）若f（x）是偶函数且函数y=f（x）的图象与函数y=h（x）的图象只有一个公共点，求实数b的取值范围．
  组卷：18引用：1难度：0.4

  解析

• 22．已知函数f（x）=（x-a）|x|+1．（其中a＞0）
  （1）若f（x）在R上有两个零点，求实数a的值；
  （2）若对任意x₁，x₂∈[-1，a-1]，使得|f（x₁）-f（x₂）|≤2a恒成立，求实数a的取值范围．
  组卷：63引用：3难度：0.4

  解析