2023-2024学年广东省东莞实验中学高二（上）月考数学试卷（10月份）

一、单项选择题：（本大题共8小题，每小题5分，共40分.每小题只有一个正确选项）

• 1．已知复数z满足（1+i）z=3+i,其中i是虚数单位，则|z|=（　　）

  A．10

  B． 10

  C．5

  D． 5
  组卷：41引用：9难度：0.9

  解析

• 2．已知直线l₁：y-3=2（x-2），则l₁在y轴上的截距为（　　）

  A．（0，1）

  B．（0，-1）

  C．1

  D．-1
  组卷：72引用：5难度：0.9

  解析

• 3．已知向量

  a

  =

  （

  0

  ，

  1

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ，

  0

  ）

  ，则向量

  b

  在向量

  a

  上的投影向量为（　　）

  A．（0，-1，-1）

  B．（-1，0，-1）

  C． （ 0 ， 1 2 ， 1 2 ）

  D． （ 1 2 ， 0 ， 1 2 ）
  组卷：212引用：8难度：0.8

  解析

• 4．设点M为不在坐标平面上的点．若点M关于坐标平面Oxz的对称点记为M₁，M₁关于坐标原点的对称点为M₂，则M关于以下哪条坐标轴对称可以得到M₂（　　）

  A．x轴

  B．y轴

  C．z轴

  D．以上都不对
  组卷：13引用：2难度：0.8

  解析

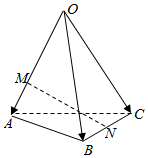• 5．如图，空间四边形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，点M在

  OA

  上，且OM=2MA，点N为BC中点，则

  MN

  =（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  组卷：2461引用：155难度：0.9

  解析

• 6．古代城池中的“瓮城”，又叫“曲池”，是加装在城门前面或里面的又一层门，若敌人攻入瓮城中，可形成“瓮中捉鳖”之势．如图的“曲池”是上、下底面均为半圆形的柱体．若AA₁⊥面ABCD，AA₁=3，AB=4，CD=2，E为弧A₁B₁的中点，则直线CE与平面DEB₁所成角的正弦值为（　　）
  

  A． 399 21

  B． 273 21

  C． 2 42 21

  D． 42 21
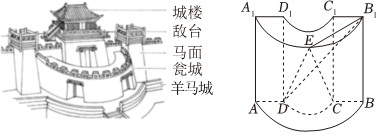  组卷：147引用：8难度：0.6

  解析

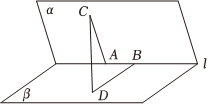• 7．如图，已知二面角α-l-β的棱上有两个点A，B，线段BD与AC分别在这个二面角的两个半平面内，且都垂直与棱l.若

  AB

  =

  4

  ，

  AC

  =

  6

  ，

  BD

  =

  8

  ，

  CD

  =

  2

  17

  ，平面α与平面β的夹角为（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  组卷：64引用：2难度：0.6

  解析

四、解答题（共6小题，满分70分）

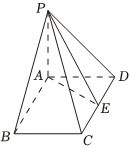• 21．如图，已知四棱锥P-ABCD的底面为边长为2的菱形，且PA⊥平面ABCD，∠ABC=60°．
  （1）设E为CD中点，证明：平面PCD⊥平面PAE；
  （2）设PA=2，PB上是否存在一点M，使得AM与平面PBC所成的角和平面AMB与平面PBC的夹角相等？若存在，求出所有满足条件的点M；若不存在，请说明理由．
  组卷：74引用：2难度：0.6

  解析

• 22．在△ABC中，设内角A，B，C所对的边分别为a,b,c.若

  AB

  •

  AC

  +

  2

  BA

  •

  BC

  =

  3

  CA

  •

  CB

  ．
  （1）证明：a²+2b²=3c²；
  （2）若sin（B-A）+sinC=7sinA，求cosA的值．
  组卷：75引用：3难度：0.5

  解析