2022-2023学年江苏省南通市海门中学高二(下)学情调研数学试卷(6月份)
发布:2024/7/4 8:0:9
一、单选题:本大题共8小题,每小题5分,共计40分.每小题给出的四个选项中,只有一项是符合要求的.
-
1.满足等式{0,1}∪X={x∈R|x3=x}的集合X共有( )
组卷:526引用:9难度:0.7 -
2.若复数z=3-4i,则
=( )z|z|组卷:408引用:5难度:0.8 -
3.若(x-a)(1-3x)3的展开式的各项系数和为8,则a=( )
组卷:706引用:3难度:0.8 -
4.函数
在[-π,π]上的图像大致为( )f(x)=x-sinxx3组卷:413引用:9难度:0.8 -
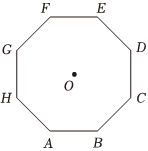 5.点P是正八边形ABCDEFGH内一点(包括边界),且=1,则|AB|的最大值为( )AB•AP组卷:68引用:2难度:0.5
5.点P是正八边形ABCDEFGH内一点(包括边界),且=1,则|AB|的最大值为( )AB•AP组卷:68引用:2难度:0.5 -
6.某中学的“信息”“足球”“摄影”三个社团考核挑选新社员,已知高一某新生对这三个社团都很感兴趣,决定三个考核都参加,假设他通过“信息”“足球”“摄影”三个社团考核的概率依次为
,m,n,且他是否通过每个考核相互独立,若三个社团考核他都通过的概率为13,至少通过一个社团考核的概率为130,则m+n=( )1115组卷:94引用:4难度:0.7 -
7.若存在斜率为3a(a>0)的直线l与曲线
与g(x)=3a2lnx都相切,则实数b的取值范围为( )f(x)=12x2+2ax-2b组卷:189引用:5难度:0.4
四、解答题:本大题共6小题,共计70分.解答时应写出文字说明、证明过程或演算步骤.
-
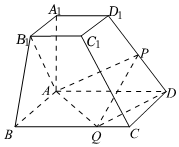 21.如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为2和4的正方形,A1A=4,且A1A⊥底面ABCD,点P、Q分别在棱DD1、BC上.
21.如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为2和4的正方形,A1A=4,且A1A⊥底面ABCD,点P、Q分别在棱DD1、BC上.
(1)若P是DD1的中点,证明:AB1⊥PQ;
(2)若PQ∥平面ABB1A1,二面角P-QD-A的余弦值为,求四面体ADPQ的体积.49组卷:523引用:15难度:0.4 -
22.已知函数
.f(x)=klnx+1ex(k∈R)
(1)若函数y=f(x)为增函数,求k的取值范围;
(2)已知0<x1<x2,
(i)证明:;eex2-eex1>1-x2x1
(ii)若,证明:|f(x1)-f(x2)|<1.x1ex1=x2ex2=k组卷:372引用:9难度:0.6


