当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省锦州市高一（下）期末数学试卷

发布：2024/6/28 8:0:9

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若z（1+2i）+i=0，则|z|=（　　）
A．
2
B．
2
2
C．
5
D．
5
5
组卷：49引用：2难度：0.8
解析
2．在△ABC中，若
A
=
2
π
3
，AB=3，则
AB
在
AC
上的投影的数量为（　　）
A．
-
3
3
2
B．
-
3
2
C．
3
2
D．
3
3
2
组卷：203引用：2难度：0.8
解析
3．《九章算术》是我国算术名著，其中有这样的一个问题：“今有宛田，下周三十步，径十六步．问为田几何？”意思是说：“现有扇形田，弧长30步，直径16步，问面积是多少？”在此问题中，扇形的圆心角的弧度数是（　　）
A．
15
4
B．
4
15
C．
15
8
D．120
组卷：475引用：9难度：0.9
解析
4．已知m,n是空间中两条不同的直线，平面α，β是两个不同的平面，下列命题中正确的是（　　）
A．若m∥n,n⊂α，则m∥α
B．若m⊥α，α⊥β，则m∥β
C．若m⊥α，m∥n,n∥β，则α⊥β
D．若m∥α，n∥α，m,n⊂β，则α∥β
组卷：82引用：8难度：0.7
解析
5．在△ABC中，角A，B，C所对的边分别是a,b,c,
a
=
7
，b=2，
A
=
π
4
，则cosB=（　　）
A．
6
3
B．
-
6
3
或
6
3
C．
35
7
D．
-
35
7
或
35
7
组卷：99引用：2难度：0.7
解析
6．x₀是函数f（x）=sinx-cos²x+1的最小值点，则sinx₀=（　　）
A．
-
1
2
B．
1
2
C．
-
1
4
D．
1
4
组卷：75引用：1难度：0.7
解析
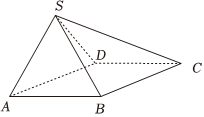7．如图，四棱锥S-ABCD的底面ABCD是菱形，且∠BAD=∠SAB=∠SAD=60°，AB=AS=2，则SC=（　　）
A．
2
B．
2
2
C．
6
D．
2
6
组卷：45引用：2难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．已知i是虚数单位，a,b∈R，设复数
z
1
=
2
a
-
3
i
，z₂=2b+i,z₃=a+bi,且|z₃|=1．
（1）若z₁-z₂为纯虚数，求z₃；
（2）若复数z₁，z₂在复平面上对应的点分别为A，B，且O为复平面的坐标原点．
①是否存在实数a,b,使向量
OB
逆时针旋转90°后与向量
OA
重合，如果存在，求实数a,b的值；如果不存在，请说明理由；
②若O，A，B三点不共线，记△ABO的面积为S（a,b），求S（a,b）及其最大值．
组卷：151引用：9难度：0.4
解析
22．如图，已知等腰梯形ABCD的外接圆半径为2，AB∥CD，AB=2CD，点P是上半圆上的动点（不包含A，B两点），点Q是线段PA上的动点，将半圆APB所在的平面沿直径AB折起使得平面PAB⊥平面ABCD．

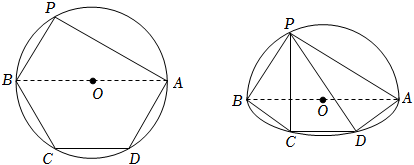
（1）求三棱锥P-ACD体积的最大值；
（2）当PC∥平面QBD时，求
|
PQ
|
|
QA
|
的值；
（3）设QB与平面ABD所成的角为α，二面角Q-BD-A的平面角为β．求证：tanβ=2tanα．
组卷：112引用：5难度：0.5
解析