当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省盐城市高三（上）段考数学试卷（11月份）

发布：2024/7/23 8:0:8

一、单项选择题：共8题，每题5分，共40分.每题只有一个选项最符合题意.

1．命题“∀x∈R，x²-x+1=0”的否定为（　　）
A．∀x∈R，x²-x+1≠0 B．∃x∈R，x²-x+1=0
C．∃x∈R，x²-x+1≠0 D．∃x∉R，x²-x+1≠0
组卷：146引用：4难度：0.8
解析
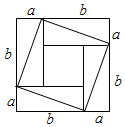2．无字证明是指禁用图象而无需文字解释就能不证自明的数学命题，由于其不证自明的特性，这种证明方式被认为比严格的数学证明更为优雅与条理，如图，请写出该图验证的不等式（　　）
A．a²+b²≥a+b B．4ab≥a²+b² C．
a
+
b
≥
2
ab
D．a²+b²≥2ab
组卷：159引用：5难度：0.5
解析
3．专家对某地区新冠肺炎爆发趋势进行研究发现，从确诊第一名患者开始累计时间t（单位：天）与病情爆发系数f（t）之间，满足函数模型：f（t）=
1
1
+
e
-
0
.
22
（
t
-
50
）
，当f（t）=0.1时，标志着疫情将要大面积爆发，则此时t约为（　　）（参考数据：e^1.1≈3）
A．38 B．40 C．45 D．47
组卷：297引用：11难度：0.7
解析
4．衡量曲线弯曲程度的重要指标是曲率，曲线的曲率定义如下：若f'（x）是f（x）的导函数，f″（x）是f'（x）的导函数，则曲线y=f（x）在点（x,f（x））处的曲率
K
=
|
f
″
（
x
）
|
（
1
+
[
f
′
（
x
）
]
2
）
3
2
•
已知f（x）=lnx-cos（x-1），则曲线y=f（x）在点（1，f（1））处的曲率为（　　）
A．0 B．
2
4
C．
2
2
D．
2
组卷：104引用：4难度：0.8
解析
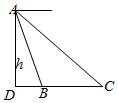5．如图，从高为h的气球（A）上测量待建规划铁桥（BC）的长，如果测得桥头（B）的俯角是α，桥头（C）的俯角是β，则桥BC的长为（　　）
A．
sin
（
α
-
β
）
sinαsinβ
h B．
cos
（
α
-
β
）
sinαsinβ
h
C．
sin
（
α
-
β
）
cosαcosβ
h D．
cos
（
α
-
β
）
cosαcosβ
h
组卷：64引用：8难度：0.7
解析
6．函数f（x）=cos（πx+φ）（0＜φ＜
π
2
）的部分图象如图所示，若方程f（x）=a在（0，x₀）上有两个不同的实数解x₁，x₂，则x₁f（x₁）+x₂f（x₂）的取值范围是（　　）
A．{0} B．（-1，
2
2
） C．（-
3
2
，
3
2
4
） D．（-
4
3
，
3
2
4
）
组卷：329引用：2难度：0.6
解析
7．已知数列{a_n}的通项公式是
a
n
=
n
2
sin
（
2
n
+
1
2
π
）
，则a₁+a₂+a₃+…+a₁₂=（　　）
A．0 B．55 C．66 D．78
组卷：134引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤

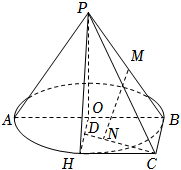21．如图，P为圆锥的顶点，O为圆锥底面的圆心，圆锥的底面直径AB=4，母线PH=2
2
，M是PB的中点，四边形OBCH为正方形．
（1）设平面POH∩平面PBC=l；证明：l∥BC；
（2）设D为OH的中点，N是线段CD上的一个点，当MN与平面PAB所成角最大时，求MN的长．
组卷：303引用：9难度：0.5
解析
22．已知函数
f
（
x
）
=
x
-
1
x
-
alnx
（
a
∈
R
）
．
（1）若函数f（x）在（2，+∞）上单调递增，求a的取值范围；
（2）若函数f（x）有两个不同的极值点x₁，x₂（x₁＞x₂），不等式f（x₁）＜mx₂恒成立，求实数m的取值范围．
组卷：99引用：4难度：0.3
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．∀x∈R，x²-x+1≠0	B．∃x∈R，x²-x+1=0
C．∃x∈R，x²-x+1≠0	D．∃x∉R，x²-x+1≠0

A． sin （ α - β ） sinαsinβ h	B． cos （ α - β ） sinαsinβ h
C． sin （ α - β ） cosαcosβ h	D． cos （ α - β ） cosαcosβ h

2022-2023学年江苏省盐城市高三（上）段考数学试卷（11月份）

一、单项选择题：共8题，每题5分，共40分.每题只有一个选项最符合题意.

1．命题“∀x∈R，x2-x+1=0”的否定为（ ）

2．无字证明是指禁用图象而无需文字解释就能不证自明的数学命题，由于其不证自明的特性，这种证明方式被认为比严格的数学证明更为优雅与条理，如图，请写出该图验证的不等式（ ）

5．如图，从高为h的气球（A）上测量待建规划铁桥（BC）的长，如果测得桥头（B）的俯角是α，桥头（C） 的俯角是β，则桥BC的长为（ ）

6．函数f（x）=cos（πx+φ）（0＜φ＜π2）的部分图象如图所示，若方程f（x）=a在（0，x0）上有两个不同的实数解x1，x2，则x1f（x1）+x2f（x2）的取值范围是（ ）

7．已知数列{an}的通项公式是an=n2sin（2n+12π），则a1+a2+a3+…+a12=（ ）

四、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤

22．已知函数f（x）=x-1x-alnx（a∈R）．（1）若函数f（x）在（2，+∞）上单调递增，求a的取值范围；（2）若函数f（x）有两个不同的极值点x1，x2（x1＞x2），不等式f（x1）＜mx2恒成立，求实数m的取值范围．

1．命题“∀x∈R，x²-x+1=0”的否定为（　　）

2．无字证明是指禁用图象而无需文字解释就能不证自明的数学命题，由于其不证自明的特性，这种证明方式被认为比严格的数学证明更为优雅与条理，如图，请写出该图验证的不等式（　　）

5．如图，从高为h的气球（A）上测量待建规划铁桥（BC）的长，如果测得桥头（B）的俯角是α，桥头（C）的俯角是β，则桥BC的长为（　　）

6．函数f（x）=cos（πx+φ）（0＜φ＜
π
2
）的部分图象如图所示，若方程f（x）=a在（0，x₀）上有两个不同的实数解x₁，x₂，则x₁f（x₁）+x₂f（x₂）的取值范围是（　　）

7．已知数列{a_n}的通项公式是
a
n
=
n
2
sin
（
2
n
+
1
2
π
）
，则a₁+a₂+a₃+…+a₁₂=（　　）

22．已知函数
f
（
x
）
=
x
-
1
x
-
alnx
（
a
∈
R
）
．
（1）若函数f（x）在（2，+∞）上单调递增，求a的取值范围；
（2）若函数f（x）有两个不同的极值点x₁，x₂（x₁＞x₂），不等式f（x₁）＜mx₂恒成立，求实数m的取值范围．