2023-2024学年江苏省苏州市姑苏区振华中学九年级(上)月考数学试卷(10月份)
发布:2024/9/12 10:0:8
一、选择题(共8小题,每题3分,共24分)
-
1.下列各式中,y是x的二次函数是( )
组卷:425引用:4难度:0.8 -
2.抛物线y=-2(x-2)2+3的顶点坐标是( )
组卷:250引用:6难度:0.6 -
3.若关于x的一元二次方程x2-2x-k=0没有实数根,则k的取值范围是( )
组卷:1277引用:49难度:0.9 -
4.在二次函数y=-(x+1)2+2的图象中,若y随x的增大而增大,则x的取值范围是( )
组卷:1049引用:4难度:0.6 -
5.在“新冠”初期,有1人感染了“新冠”,经过两轮传染后共有324人感染了“新冠”(这两轮感染均未被发现未被隔离),则每轮传染中平均一个人传染了几个人?设每轮传染中平均一个人传染了x人,则根据题意可列方程( )
组卷:176引用:1难度:0.5 -
6.抛物线y=-x2+bx+3的对称轴为直线x=-1,若关于x的一元二次方程-x2+bx+3-t=0(t为实数)在-2<x<3的范围内有实数根,则t的取值范围是( )
组卷:5178引用:24难度:0.3 -
7.抛物线y=(m+1)x2+2mx+3上有两点A(-3,y1)、B(5,y2)、C点(x0,y0)为此抛物线顶点且y1>y2≥y0,则m的取值范围为( )
组卷:590引用:3难度:0.5 -
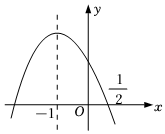 8.如图,抛物线y=ax2+bx+c的对称轴为直线x=-1,且过点(,0),有下列结论:①abc>0;②a-2b+4c>0;③25a-10b+4c=0;④3b+2c>0;其中正确的结论有( )12组卷:425引用:3难度:0.5
8.如图,抛物线y=ax2+bx+c的对称轴为直线x=-1,且过点(,0),有下列结论:①abc>0;②a-2b+4c>0;③25a-10b+4c=0;④3b+2c>0;其中正确的结论有( )12组卷:425引用:3难度:0.5
二、填空题(共8小题,每题3分,共24分)
-
9.关于x的方程x2=x的解是 .
组卷:49引用:3难度:0.7
三、解答题(共11小题,共82分)
-
26.定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则这两个函数互为“N”函数.
(1)写出y=-x2+x-1的“N”函数的表达式;
(2)若题(1)中的两个“N”函数与正比例函数y=kx(k≠0)的图象只有两个交点,求k的值;
(3)如图,二次函数y1与y2互为“N”函数,A、B分别是“N”函数y1与y2图象的顶点,C是“N”函数y2与y轴正半轴的交点,连接AB、AC、BC,若点A(-2,1)且△ABC为直角三角形,求点C的坐标.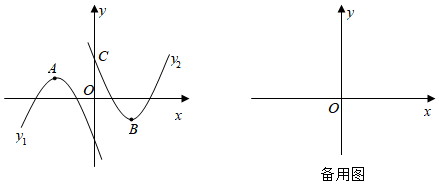 组卷:980引用:5难度:0.1
组卷:980引用:5难度:0.1 -
27.综合与实践
问题提出
某兴趣小组开展综合实践活动:在Rt△ABC中,∠C=90°,D为AC上一点,CD=,动点P以每秒1个单位的速度从C点出发,在三角形边上沿C→B→A匀速运动,到达点A时停止,以DP为边作正方形DPEF.设点P的运动时间为t s,正方形DPEF的面积为S,探究S与t的关系.2
初步感知
(1)如图1,当点P由点C运动到点B时,
①当t=1时,S=;
②S关于t的函数解析式为 .
(2)当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象.请根据图象信息,求S关于t的函数解析式及线段AB的长.
延伸探究
(3)若存在3个时刻t1,t2,t3(t1<t2<t3)对应的正方形DPEF的面积均相等.
①t1+t2=;
②当t3=4t1时,求正方形DPEF的面积.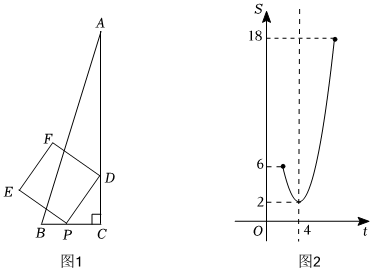 组卷:3553引用:27难度:0.3
组卷:3553引用:27难度:0.3


