2022-2023学年吉林省松原市宁江区四校九年级（下）期中数学试卷

一、单项选择题（每小题2分，共12分)

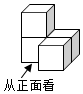
• 1．如图是由4个相同的小正方体组成的一个立体图形，其主视图是（　　）
  

  A．

  B．

  C．

  D．
  组卷：700引用：24难度：0.8

  解析

• 2．如图，数轴上表示-2的点A到原点的距离是（　　）

  A．-2

  B．2

  C．- 1 2

  D． 1 2
  组卷：2932引用：21难度：0.9

  解析

• 3．下列运算一定正确的是（　　）

  A．2a+2a=2a2	B．a2•a3=a6
  C．（2a2）3=6a6	D．（a+b）（a-b）=a2-b2
  组卷：876引用：28难度：0.8

  解析

• 4．不等式组

  x + 1 ≥ 2

  9 - x ＜ 2 x

  的解集在数轴上表示正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：626引用：7难度：0.6

  解析

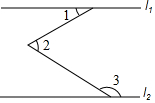• 5．如图，直线l₁∥l₂，∠1=30°，则∠2+∠3=（　　）

  A．150°

  B．180°

  C．210°

  D．240°
  组卷：3038引用：29难度：0.5

  解析

• 6．《九章算术》中有这样一个题：今有甲乙二人持钱不知其数．甲得乙半而钱五十，乙得甲太半而钱亦五十．问甲、乙持钱各几何？其意思为：今有甲乙二人，不知其钱包里有多少钱，若乙把其一半的钱给甲，则甲的钱数为50；而甲把其

  2

  3

  的钱给乙，则乙的钱数也为50，问甲、乙各有多少钱？设甲的钱数为x,乙的钱数为y,则可建立方程组为（　　）

  A． x + 1 2 y = 50 2 3 x + y = 50	B． x + 1 2 y = 50 x + 2 3 y = 50
  C． 1 2 x + y = 50 2 3 x + y = 50	D． 1 2 x + y = 50 x + 2 3 y = 50
  组卷：2457引用：40难度：0.6

  解析

二、填空题（每小题3分，共24分）

• 7．计算：（-

  1

  3

  -

  1

  2

  ）÷

  5

  4

  =

  ．
  组卷：1450引用：28难度：0.8

  解析

• 8．分解因式：x³+5x²+6x=

  ．
  组卷：3997引用：14难度：0.7

  解析

六、解答题（每小题10分，共20分）

• 25．如图，在矩形ABCD中，AB=8cm,AD=4cm,对角线AC，BD交于点O，动点P，Q分别从点A出发，点P沿A-D-C以3cm/s的速度运动，同时点Q沿A-O-B以

  5

  cm/s速度运动，其中一点到达终点，另一动点随之停止运动，连结AP，AQ，PQ．设运动时间为t（s），△APQ的面积为S（cm²）．
  （1）求线段PD的长（用含t的式子表示）．
  （2）当AP平分∠DAC时，直接写出t的值．
  （3）求S与t的函数关系式，并写出自变量的取值范围．
  （4）当△APQ是等腰三角形时，直接写出t的值．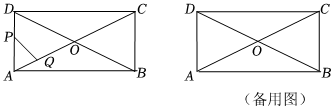
  
  组卷：23引用：1难度：0.2

  解析

• 26．如图，在平面直角坐标系中，一次函数y=kx+b与二次函数y=-x²+mx+n交于点A（3，0），B（0，3）两点．
  （1）求一次函数y=kx+b和二次函数y=-x²+mx+n的解析式．
  （2）点P是二次函数图象上一点，且位于直线AB上方，过点P作y轴的平行线，交直线AB于点Q，当△PAB面积最大时，求点P的坐标．
  （3）点M在二次函数图象上，点N在二次函数图象的对称轴上，若以点A、B、M、N为顶点的四边形是平行四边形时，求点M的坐标．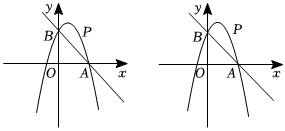
  
  组卷：383引用：2难度：0.4

  解析