2023年辽宁省丹东市高考数学质检试卷(一)
发布:2024/7/1 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A={x∈N*|(x+1)(x-a)≤0},B={-3,-2,1},若A⊆B且A∩B≠∅,则a=( )
组卷:177引用:2难度:0.7 -
2.下列函数中为偶函数的是( )
组卷:188引用:2难度:0.7 -
3.已知向量
=(2,1),a=(-3,4),则b在a方向上的投影是( )b组卷:172引用:3难度:0.8 -
4.图1是世界上单口径最大、灵敏度最高的射电望远镜“中国天眼”——500m口径抛物面射电望远镜,反射面的主体是一个抛物面(抛物线绕其对称轴旋转所形成的曲面称为抛物面),其边缘距离底部的落差约为156.25米,它的一个轴截面是一个开口向上的抛物线C的一部分,放入如图2所示的平面直角坐标系xOy内,已知该抛物线上点P到底部水平线(x轴)距离为125m,则点P到该抛物线焦点F的距离为( )
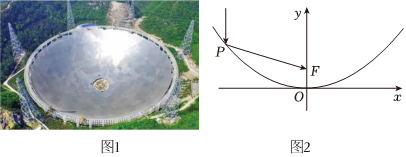 组卷:90引用:3难度:0.7
组卷:90引用:3难度:0.7 -
5.
的值为( )1+sin10组卷:198引用:2难度:0.5 -
6.已知函数f(x)的定义域为D,若对任意的x∈D,都存在x0∈D,使得x+f(x0)=1,则“f(x)存在零点”是“1∈D”的( )
组卷:64引用:3难度:0.7 -
7.设C'与C分别为圆柱上下底面圆周上的点,且位于该圆柱轴截面ABB'A'同侧,下底面圆心O在AB上,若
,ˆBC=2ˆCA,ˆA′C′=2ˆC′B′,则直线CC'与AB所成角的余弦值为( )cos∠C′CO=13组卷:42引用:2难度:0.5
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
-
21.已知O为坐标原点,F1(-2,0),F2(2,0)为双曲线C:
的左右焦点,P为C的右支上一点,当PF2⊥x轴时,x2a2-y2b2=1(a>0,b>0).|OP|=13
(1)求C的方程;
(2)若P异于C的右顶点A,点Q在直线上,AP∥OQ,M为AP的中点,直线OM与直线QF2的交点为N,求|NF1|的取值范围.x=12组卷:46引用:2难度:0.4 -
22.已知函数
,f(x)=1-x1+x+alnx.a>13
(1)当时,讨论f(x)的单调性;a=38
(2)若f(x)有三个不同的零点x1,x2,x3,求a的取值范围,并证明:.3<x1+x2+x3<3-3a3a-1组卷:75引用:2难度:0.2


