当前位置：试卷中心 > 试卷详情

2022-2023学年湖北省武汉市武钢三中高二（下）月考数学试卷（3月份）

发布：2024/7/6 8:0:9

一、单选题（每小题5分，共40分）

1．设a∈N，且a＜17，若52²⁰²²+a能被17整除，则a等于（　　）
A．0 B．1 C．13 D．16
组卷：266引用：4难度：0.8
解析
2．若函数f（x）=2x²-lnx在其定义域的一个子区间（2k-1，2k+1）内不是单调函数，则实数k的取值范围是（　　）
A．
[
1
2
，
3
4
）
B．
[
3
4
，
+
∞
）
C．
[
1
2
，
2
）
D．
（
-
1
2
，
3
4
）
组卷：97引用：4难度：0.6
解析
3．11月29日，江西新余仙女湖的渔民们迎来入冬第一个开捕日，仙女湖的有机鱼迎来又一个丰收年．七位渔民分在一个小组，各驾驶一辆渔船依次进湖捕鱼，甲乙渔船要排在一起出行，丙必须在最中间出行，则不同的排法有（　　）
A．96种 B．120种 C．192种 D．240种
组卷：235引用：4难度：0.7
解析
4．若（1-2x）²⁰²²=a₀+a₁（x+1）+a₂（x+1）²+...+a₂₀₂₂（x+1）²⁰²²，则
a
2022
a
0
=（　　）
A．2²⁰²² B．（
1
2
）²⁰²² C．（
2
3
）²⁰²² D．（
3
2
）²⁰²²
组卷：161引用：1难度：0.7
解析
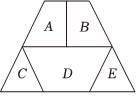5．用红、黄、蓝、绿、橙五种不同颜色给如图所示的5块区域A、B、C、D、E涂色，要求同一区域用同一种颜色，有公共边的区域使用不同颜色，则共有涂色方法（　　）
A．120种 B．720种 C．840种 D．960种
组卷：125引用：2难度：0.7
解析
6．已知函数y=f（x）对任意的
x
∈
（
-
π
2
，
π
2
）
满足f'（x）cosx-f（x）sinx＞0（其中f'（x）是函数f（x）的导函数），则下列不等式成立的是（　　）
A．
f
（
-
π
3
）
＞
2
f
（
-
π
4
）
B．
f
（
π
3
）
＜
2
f
（
π
4
）
C．
2
f
（
0
）
＜
f
（
π
3
）
D．
2
f
（
0
）
＞
f
（
π
4
）
组卷：169引用：9难度：0.5
解析
7．已知双曲线E：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的右顶点为A，抛物线C：y²=12ax的焦点为F．若在双曲线的渐近线上存在一点P，使得
PA
•
PF
=0，则双曲线E的离心率的取值范围是（　　）
A．（1，2） B．（1，
2
3
3
] C．（2，+∞） D．[
2
3
3
，+∞）
组卷：153引用：8难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（共70分）

21．已知过点（1，e）的椭圆E：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的焦距为2，其中e为椭圆E的离心率．
（1）求E的标准方程；
（2）设O为坐标原点，直线l与E交于A，C两点，以OA，OC为邻边作平行四边形OABC，且点B恰好在E上，试问：平行四边形OABC的面积是否为定值？若是定值，求出此定值；若不是，说明理由．
组卷：185引用：6难度：0.5
解析
22．已知函数f（x）=xlnx-1，g（x）=ax²-（a-2）x.
（1）求f（x）的最小值；
（2）设函数h（x）=f'（x）-g（x），讨论h（x）的单调性；
（3）设函数G（x）=g（x）+（a-2）x,若f（x）的图象与G（x）的图象有A（x₁，y₁），B（x₂，y₂）两个不同的交点，证明：ln（x₁x₂）＞2+ln2．
组卷：76引用：4难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． f （ - π 3 ）＞ 2 f （ - π 4 ）	B． f （ π 3 ）＜ 2 f （ π 4 ）
C． 2 f （ 0 ）＜ f （ π 3 ）	D． 2 f （ 0 ）＞ f （ π 4 ）

2022-2023学年湖北省武汉市武钢三中高二（下）月考数学试卷（3月份）

一、单选题（每小题5分，共40分）

1．设a∈N，且a＜17，若522022+a能被17整除，则a等于（ ）

2．若函数f（x）=2x2-lnx在其定义域的一个子区间（2k-1，2k+1）内不是单调函数，则实数k的取值范围是（ ）

4．若（1-2x）2022=a0+a1（x+1）+a2（x+1）2+...+a2022（x+1）2022，则a2022a0=（ ）

5．用红、黄、蓝、绿、橙五种不同颜色给如图所示的5块区域A、B、C、D、E涂色，要求同一区域用同一种颜色，有公共边的区域使用不同颜色，则共有涂色方法（ ）

6．已知函数y=f（x）对任意的x∈（-π2，π2）满足f'（x）cosx-f（x）sinx＞0（其中f'（x）是函数f（x）的导函数），则下列不等式成立的是（ ）

7．已知双曲线E：x2a2-y2b2=1（a＞0，b＞0）的右顶点为A，抛物线C：y2=12ax的焦点为F．若在双曲线的渐近线上存在一点P，使得PA•PF=0，则双曲线E的离心率的取值范围是（ ）

四、解答题（共70分）

1．设a∈N，且a＜17，若52²⁰²²+a能被17整除，则a等于（　　）

2．若函数f（x）=2x²-lnx在其定义域的一个子区间（2k-1，2k+1）内不是单调函数，则实数k的取值范围是（　　）

4．若（1-2x）²⁰²²=a₀+a₁（x+1）+a₂（x+1）²+...+a₂₀₂₂（x+1）²⁰²²，则
a
2022
a
0
=（　　）

5．用红、黄、蓝、绿、橙五种不同颜色给如图所示的5块区域A、B、C、D、E涂色，要求同一区域用同一种颜色，有公共边的区域使用不同颜色，则共有涂色方法（　　）

6．已知函数y=f（x）对任意的
x
∈
（
-
π
2
，
π
2
）
满足f'（x）cosx-f（x）sinx＞0（其中f'（x）是函数f（x）的导函数），则下列不等式成立的是（　　）

7．已知双曲线E：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的右顶点为A，抛物线C：y²=12ax的焦点为F．若在双曲线的渐近线上存在一点P，使得
PA
•
PF
=0，则双曲线E的离心率的取值范围是（　　）