2023-2024学年江苏省无锡市锡山区二泉中学八年级（上）段考数学试卷（10月份）

一、选择题（本大题共10小题，每小题3分，共30分）

• 1．下面四个图形中，属于轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1408引用：28难度：0.8

  解析

• 2．数9的算术平方根是（　　）

  A．±3

  B． 3

  C．-3

  D．3
  组卷：405引用：7难度：0.8

  解析

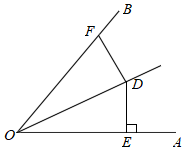• 3．如图，OD平分∠AOB，DE⊥AO于点E，DE=4，点F是射线OB上的任意一点，则DF的长度不可能是（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：1742引用：19难度：0.8

  解析

• 4．如图，将两根同样的钢条AC和BD的中点O固定在一起，使其可以绕着O点自由转动，就做成了一个测量工件内径的工具．这时根据△OAB≌△OCD，CD的长就等于工件内槽的宽AB，这里判定△OAB≌△OCD的依据是（　　）

  A．SAS

  B．ASA

  C．SSS

  D．AAS
  组卷：651引用：5难度：0.7

  解析

• 5．在联欢会上，有A、B、C三名选手站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在△ABC的（　　）

  A．三边中线的交点	B．三条角平分线的交点
  C．三边中垂线的交点	D．三边上高的交点
  组卷：4074引用：68难度：0.9

  解析

• 6．若[a]表示数a的整数部分，例如[π]=3，则[

  24

  ]=（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：215引用：4难度：0.7

  解析

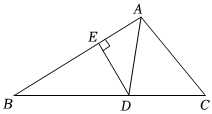• 7．如图，AD是△BAC的平分线，DE⊥AB于点E，S_△ABC=32，DE=4，AB=9，则AC的长是（　　）

  A．6

  B．7

  C．8

  D．9
  组卷：731引用：7难度：0.7

  解析

• 8．如图所示，把长方形ABCD沿EF对折，若∠1=50°，则∠AEF的度数为（　　）

  A．65°

  B．115°

  C．130°

  D．120°
  组卷：131引用：8难度：0.6

  解析

三．解答题（本大题共7小题，共66分．请在答题卷指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

• 24．如图，∠AOB=30°，点M，N在边OA上，点N在点M的上方，MN=2，点M从O开始沿着射线OA移动，移动距离为x,点P是边OB上的点．
  （1）利用直尺和圆规在图中确定点P，使得PM=PN；
  （2）在整个移动过程中，使P、M、N构成等腰三角形的点P最少有

  个，最多有

  个；当x=2时，这样的点P有

  个．
  （3）若使P、M、N构成等腰三角形的点P恰好有3个，写出x满足的条件．
  
  组卷：501引用：2难度：0.5

  解析

• 25．以△ABC的AB、AC为边作△ABD和△ACE，且AE=AB，AC=AD，CE与BD相交于M，∠EAB=∠CAD=α．
  
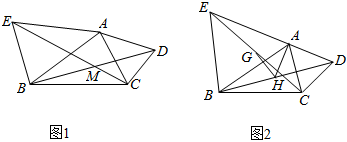
  （1）如图1，求证：△AEC≌△ABD；
  （2）在图1中，连接AM，则∠EMB=

  ，∠AMC=

  ；（都用含α的代数式表示）
  （3）如图2，若α=50°，G、H分别是EC、BD的中点，求∠AHG的度数．
  组卷：1010引用：3难度：0.5

  解析