如图，∠AOB=30°，点M，N在边OA上，点N在点M的上方，MN=2，点M从O开始沿着射线OA移动，移动距离为x,点P是边OB上的点．
（1）利用直尺和圆规在图中确定点P，使得PM=PN；
（2）在整个移动过程中，使P、M、N构成等腰三角形的点P最少有 11个，最多有 44个；当x=2时，这样的点P有 11个．
（3）若使P、M、N构成等腰三角形的点P恰好有3个，写出x满足的条件．
【答案】1；4；1
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/19 21:0:8组卷：501引用：2难度：0.5
相似题
-
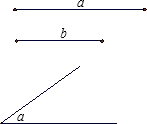1．尺规作图：
已知线段a,b和∠α．
求作：△ABC，使BC=a,AC=b,∠C=∠α
（画出图形，保留作图痕迹，不写作法，写出结论）发布：2025/6/18 11:30:2组卷：125引用：6难度：0.5 -
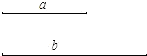2．如图，已知线段a、b,求作：Rt△ABC，使∠ACB=90°，BC=a,AC=b（不写作法，保留作图痕迹）．发布：2025/6/18 11:30:2组卷：106引用：7难度：0.3 -
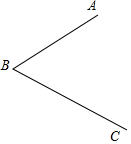3．如图，
（1）在图中求作⊙O，使⊙O满足以线段AB为弦，且圆心O到∠ABC两边的距离相等（要求：尺规作图，不写作法，保留作图痕迹）；
（2）若AB=2，∠ABC=60°，请求出（1）中所作的⊙O的半径．3发布：2025/6/18 13:0:8组卷：148引用：2难度：0.5
