2022-2023学年山东省聊城市高一（上）期中数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．设A={3，5，6，8}，B={4，5，7，8}，则A∩B的结果为（　　）

  A．{5}	B．{3，4，5，6，7，8}
  C．{8}	D．{5，8}
  组卷：46引用：8难度：0.9

  解析

• 2．命题“∃x∈R，

  x

  2

  +

  x

  2

  ≤

  0

  ”的否定是（　　）

  A．∃x∈R， x 2 + x 2 ≥ 0	B．∃x∈R， x 2 + x 2 ＞ 0
  C．∀x∈R， x 2 + x 2 ＞ 0	D．∀x∈R， x 2 + x 2 ≤ 0
  组卷：1引用：2难度：0.7

  解析

• 3．设集合A={x|x²＜3，x∈Z}，则A的真子集共有（　　）

  A．8个

  B．7个

  C．4个

  D．3个
  组卷：9引用：2难度：0.7

  解析

• 4．使|x+1|＞2成立的一个必要不充分条件是（　　）

  A．x＜-3

  B．x＞0

  C．x＜-3或x＞1

  D．x＜-3或x＞0
  组卷：122引用：3难度：0.7

  解析

• 5．设集合P，Q都是实数集R的子集，且P∩（∁_RQ）=∅，则P∩Q=（　　）

  A．∅

  B．R

  C．Q

  D．P
  组卷：5引用：3难度：0.7

  解析

• 6．已知函数f（x）=4kx²-x-8在[5，20]上单调递增，则实数k的取值范围为（　　）

  A． k ≥ 1 40

  B．k＜0

  C． k ≥ 1 40 或k＜0

  D． k ≥ 1 40 或k≤0
  组卷：18引用：2难度：0.7

  解析

• 7．已知a＞0，b＞0，且ab=1，不等式

  1

  2

  a

  +

  1

  2

  b

  +

  m

  a

  +

  b

  ≥4恒成立，则正实数m的取值范围是（　　）

  A．[2，+∞）

  B．[4，+∞）

  C．[6，+∞）

  D．[8，+∞）
  组卷：179引用：4难度：0.8

  解析

四、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）

• 21．某服装厂计划投入80万元，全部用于甲、乙两种服装的生产，每种服装生产至少要投入10万元．在对市场进行调研分析发现生产甲服装的收益M，生产乙服装的收益N与投入a（单位：万元），满足

  M

  =

  4 a + 25 ， 10 ≤ a ≤ 49

  40 ， 49 ＜ a ≤ 70

  ，

  N

  =

  1

  2

  a

  +

  20

  ．设投入x（单位：万元）生产甲服装，两种服装的总收益为y.
  （1）当甲服装的投入为36万元时，求生产两种服装的总收益；
  （2）试问如何安排两种服装的生产投入，才能使总收益最大？
  组卷：2引用：2难度：0.7

  解析

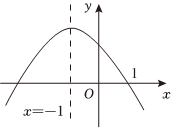• 22．已知二次函数f（x）=ax²-bx+1+b的图象如图：
  （1）求实数a,b的值；
  （2）若g（x）=

  f

  （

  x

  ）

  x

  +m为奇函数，求实数m的值；
  （3）若v（x）=

  f

  （

  x

  ）

  -

  m

  x

  ≥0在[-3，-1]上恒成立，求实数m的取值范围．
  组卷：7引用：2难度：0.6

  解析