2023-2024学年黑龙江省哈尔滨九中高二（上）月考数学试卷（9月份）

一、选择题（本大题共8小题，每小题5分，共40分，每小题分别给出四个选项，只有一个选项符合题意）

• 1．空间向量

  OA

  -

  OB

  +

  AC

  =（　　）

  A． AB

  B． CB

  C． OC

  D． BC
  组卷：234引用：5难度：0.7

  解析

• 2．点A（3，4，5）关于坐标平面Oyz对称的点B的坐标为（　　）

  A．（3，4，-5）

  B．（-3，4，5）

  C．（-3，4，-5）

  D．（-3，-4，-5）
  组卷：25引用：4难度：0.8

  解析

• 3．设向量

  a

  、

  b

  、

  c

  不共面，则下列集合可作为空间的一个基底的是（　　）

  A．{ a + b ， b - a ， a }	B．{ a + b ， b - a ， b }
  C．{ a + b ， b - a ， c }	D．{ a + b +c, a + b ， c }
  组卷：343引用：14难度：0.9

  解析

• 4．已知空间向量

  a

  =（2，-2，1），

  b

  =（3，0，4），则向量

  b

  在向量

  a

  上的投影向量是（　　）

  A． 10 9 （3，0，4）	B． 2 5 （3，0，4）
  C． 10 9 （2，-2，1）	D． 2 5 （2，-2，1）
  组卷：192引用：9难度：0.7

  解析

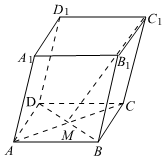• 5．如图，平行六面体ABCD-A₁B₁C₁D₁中，AC与BD的交点为点M，设

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则下列向量中与

  C

  1

  M

  相等的向量是（　　）

  A．- 1 2 a + 1 2 b + c

  B． 1 2 a + 1 2 b + c

  C．- 1 2 a - 1 2 b - c

  D．- 1 2 a - 1 2 b + c
  组卷：289引用：28难度：0.8

  解析

• 6．已知

  a

  =（1-t,2t-1，0），

  b

  =（2，t,t），则|

  b

  -

  a

  |的最小值为（　　）

  A． 5

  B． 6

  C． 2

  D． 3
  组卷：1114引用：28难度：0.7

  解析

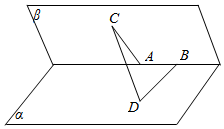• 7．如图所示，已知在一个60°的二面角的棱上，有两个点A，B，AC，BD分别是在这个二面角的两个面内垂直于AB的线段，且AB=4cm,AC=6cm,BD=8cm,则CD的长为（　　）

  A．2 17

  B．2 41

  C．2

  D．10
  组卷：132引用：5难度：0.9

  解析

四．解答题（本大题共6题，满分70分解答应写出必要的文字说明、证明过程和演算步骤）

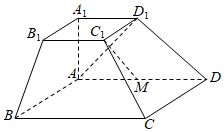• 21．如图，在四棱台ABCD-A₁B₁C₁D₁中，底面ABCD是菱形，AA₁=A₁B₁=

  1

  2

  AB=1，∠ABC=60°，AA₁⊥平面ABCD．
  （1）若点M是AD的中点，求证：C₁M∥平面AA₁B₁B；
  （2）棱BC上是否存在一点E，使得二面角E-AD₁-D的余弦值为

  1

  3

  ？若存在，求线段CE的长；若不存在，请说明理由．
  组卷：473引用：8难度：0.4

  解析

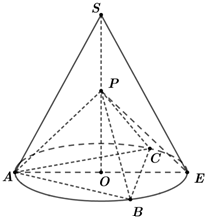• 22．如图，圆锥SO，S为顶点，O是底面的圆心，AE为底面直径，AE=AS，圆锥高SO=6，点P在高SO上，△ABC是圆锥SO底面的内接正三角形．
  （1）若PO=

  6

  ，判断PA和平面PBC是否垂直，并证明；
  （2）点P在高SO上的动点，当PE和平面PBC所成角的正弦值最大时，求三棱锥P-ABC的体积．
  组卷：93引用：4难度：0.4

  解析