2022-2023学年上海市普陀区宜川中学高二（下）期末数学试卷

一、填空题（本大题满分54分）本大题共有12题。考生应在答题纸相应编号的空格内直接填写结果，1-6题每个空格填对得4分，7-12题每个空格填对得5分，否则一律得零分。

• 1．设集合A={1，3，5，7，9}，B={x|2≤x≤5}，则A∩B=

  ．
  组卷：369引用：3难度：0.9

  解析

• 2．不等式|x-1|≤2的解集为：

  ．（结果用集合或区间表示）
  组卷：331引用：7难度：0.7

  解析

• 3．已知直线l经过点

  A

  （

  3

  ，

  3

  ）

  、

  B

  （

  3

  ，

  1

  ）

  ．直线l的倾斜角是

  ．
  组卷：123引用：3难度：0.7

  解析

• 4．已知

  π

  2

  ＜

  θ

  ＜

  π

  ，且

  cosθ

  =

  -

  4

  5

  ，则tan2θ=

  ．
  组卷：169引用：2难度：0.7

  解析

• 5．设随机变量X服从正态分布N（2，σ²），若P（X≤1）=0.2，则P（X＜3）=

  ．
  组卷：328引用：8难度：0.8

  解析

• 6．某小组成员的年龄分布茎叶图如图所示，则该小组成员年龄的第25百分位数是

  ．
  组卷：178引用：7难度：0.9

  解析

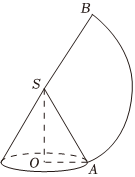• 7．如图所示，圆锥SO的底面圆半径OA=1，侧面的平面展开图的面积为3π，则此圆锥的体积为

  ．
  组卷：370引用：9难度：0.7

  解析

三、解答题（本大题满分78分）本大题共有5题，解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤。

• 20．已知抛物线Γ：y²=4x.
  （1）求抛物线Γ的焦点F的坐标和准线l的方程；
  （2）过焦点F且斜率为

  1

  2

  的直线与抛物线Γ交于两个不同的点A、B，求线段AB的长；
  （3）已知点P（1，2），是否存在定点Q，使得过点Q的直线与抛物线Γ交于两个不同的点M、N（均不与点P重合），且以线段MN为直径的圆恒过点P？若存在，求出点Q的坐标；若不存在，请说明理由．
  组卷：384引用：7难度：0.2

  解析

• 21．已知函数

  f

  （

  x

  ）

  =

  1

  2

  x

  2

  -

  （

  a

  +

  1

  ）

  x

  +

  alnx

  ．（其中a为常数）．
  （1）若a=-2，求曲线y=f（x）在点（2，f（2））处的切线方程；
  （2）当a＜0时，求函数y=f（x）的最小值；
  （3）当0≤a＜1时，试讨论函数y=f（x）的零点个数，并说明理由．
  组卷：1159引用：7难度：0.9

  解析