当前位置：试卷中心 > 试卷详情

2023-2024学年天津市西青区杨柳青一中高二（上）第二次段考数学试卷

发布：2024/10/4 1:0:1

一、选择题：在每小题给出的四个选项中，只有一项是符合题目的要求

1．若直线ax+y-a+1=0与直线（a-2）x-3y+a=0垂直，则实数a的值为（　　）
A．-1或3 B．1或-3 C．-1或-3 D．1或3
组卷：290引用：9难度：0.8
解析
2．如果方程kx²+y²=2表示焦点在x轴上的椭圆，那么实数k的取值范围是（　　）
A．（1，+∞） B．（1，2） C．
（
1
2
，
1
）
D．（0，1）
组卷：184引用：4难度：0.8
解析
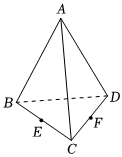3．如图，在空间四边形ABCD中，设E，F分别是BC，CD的中点，则
AB
+
1
2
（
BC
+
BD
）
=（　　）
A．
AD
B．
EF
C．
AE
D．
AF
组卷：61引用：3难度：0.7
解析
4．若圆C的半径为1，圆心在第一象限，且与直线4x-3y=0和x轴都相切，则该圆的标准方程是（　　）
A．（x-2）²+（y-1）²=1 B．（x-2）²+（y+1）²=1
C．（x+2）²+（y-1）²=1 D．（x-3）²+（y-1）²=1
组卷：821引用：50难度：0.9
解析
5．与3x+4y=0垂直，且与圆（x-1）²+y²=4相切的一条直线是（　　）
A．4x-3y=6 B．4x-3y=-6 C．4x+3y=6 D．4x+3y=-6
组卷：514引用：9难度：0.8
解析
6．古希腊几何学家阿波罗尼斯证明过这样一个命题：平面内到两定点距离之比为常数k（k＞0，k≠1）的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆．在平面直角坐标系xOy中，A（-4，0），B（2，0），点M满足
|
MA
|
|
MB
|
=
2
，则点M的轨迹方程为（　　）
A．（x+4）²+y²=16 B．（x-4）²+y²=16
C．x²+（y+4）²=16 D．x²+（y-4）²=16
组卷：192引用：4难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：本大题共3小题，共45分．解答应写出文字说明，证明过程或演算步骤．

18．已知椭圆E：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线l：y=-x+3与椭圆E相切于点T．
（1）求椭圆E的离心率；
（2）求椭圆E的标准方程及点T的坐标；
（3）设O为坐标原点，直线l'平行于直线OT，与椭圆E交于不同的两点A、B，且与直线l交于点P，那么是否存在常数λ，使得|PT|²=λ|PA|•|PB|？如果存在，求出λ的值；如果不存在，请说明理由．
组卷：501引用：4难度：0.5
解析

附如题：本题10分．请将正确的答案填写到答题纸上．

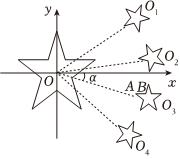19．1949年公布的《国旗制法说明》中就五星的位置规定：大五角星有一个角尖正向上方，四颗小五角星均各有一个角尖正对大五角星的中心点．有人发现，第三颗小星的姿态与大星相近．为便于研究，如图，以大星的中心点为原点，建立直角坐标系，OO₂，OO₂，OO₃，OO₄分别是大星中心点与四颗小星中心点的连接线，α≈16°，求第三颗小星的一条边AB所在直线的倾斜角？
组卷：83引用：1难度：0.7
解析