2017-2018学年重庆市九龙坡区育才中学九年级（上）第一次月考数学试卷

一、选择题：（本大题共12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

• 1．在实数-3，-2，0，-4中，最小的数是（　　）

  A．-3

  B．2

  C．0

  D．-4
  组卷：8引用：2难度：0.9

  解析

• 2．下列图形中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1403引用：246难度：0.9

  解析

• 3．计算（-2x³y）²的结果是（　　）

  A．4x5y2

  B．-4x5y2

  C．4x6y2

  D．-4x6y2
  组卷：305引用：7难度：0.9

  解析

• 4．下列调查中，最适合采用全面调查（普查）方式的是（　　）

  A．对某批节能点灯的使用寿命的调查

  B．对重庆市初三学生每天的体育锻炼时间的调查

  C．对某校九年级3班学生一周使用手机时间的调查

  D．对中秋节期间市场上某品牌月饼在我市销售情况的调查
  组卷：9引用：2难度：0.9

  解析

• 5．估计

  7

  -

  1

  2

  的值应在（　　）

  A．0.70和0.75之间	B．0.75和0.80之间
  C．0.80和0.85之间	D．0.85和0.90之间
  组卷：21引用：2难度：0.9

  解析

• 6．若y=-

  1

  3

  是关于的方程2x-3y=-3的解，则x值为（　　）

  A．-2

  B．- 11 9

  C．-1

  D． 7 9
  组卷：35引用：1难度：0.7

  解析

• 7．要使分式

  x

  +

  4

  x

  -

  3

  有意义，x应满足的条件是（　　）

  A．x＞3

  B．x＞3且x≠4

  C．x≥3

  D．x≥3且x≠4
  组卷：107引用：1难度：0.9

  解析

• 8．△ABC∽△DEF，且它们的周长之比为2：3，则它们的面积之比为（　　）

  A．2：3

  B．4：6

  C．4：9

  D．3：2
  组卷：45引用：3难度：0.7

  解析

五、解答题：（本大题2个小题，第25小题10分，第26小题12分，共22分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上．

• 25．对任意一个三位数P，将它任意两个数位上的数字对调后得到一个首位不为0的新的三位数q（q可以与P相同），记q=

  abc

  ，在所有可能的情况中，当|a-2b+c|最小时，我们称此时的q是p“幸福快乐数”，并规定：K（p）=a²-2b²+c²．例如：318按上述方法可得新数有381、813、138，因为|3-2×8+1|=12，|8-2×1+3|=9，|1-2×3+8|=3，而3＜9＜12，所以138是318的“幸福快乐数”，
  此时K（318）=1²-2×3²+8²=47．
  （1）计算：K（168），K（243）：
  （2）若m=100x+10y+8（1≤x≤y≤9，x、y都是正整数），交换其十位与百位上的数字得到新数n,若m+n是13的倍数时，求K（n）的最大值．
  组卷：410引用：2难度：0.6

  解析

• 26．如图1，二次函数y=ax²-2x+c（a≠0）的图象交x轴于点A（-1，0）、B（3，0）两点，与y轴交于点C，点D是抛物线的顶点，DH⊥x轴于点H连接AC，BC．
  （1）求抛物线的解析式；
  （2）如图2，点P是抛物线第一象限上一点，且满足△PBC的面积等于△ABC的面积．
  ①求点P的坐标；②点Q与点C关于直线DH对称，在x轴上找一点E，使得|EP-EQ|的值最大，求点E坐标以及这个最大值；
  （3）如图3，在（2）问的条件下，设直线PE交y轴于点G，交直线DH于点F，y轴上有一定点M（0，4），点K为PQ的中点，连接MF，先将△MFG沿着直线MF翻折到△MFN，再将抛物线y=ax²-2x+c沿着其对称轴DH向上平移，得到抛物线y₁，使得抛物线y₁的图象刚好过点N，此时抛物线y₁交y轴于点T，连接TK．请问在直线PE上是否存在一点Y，使得△TKY是直角三角形？若存在，请直接写出点Y的坐标；若不存在，请说明理由．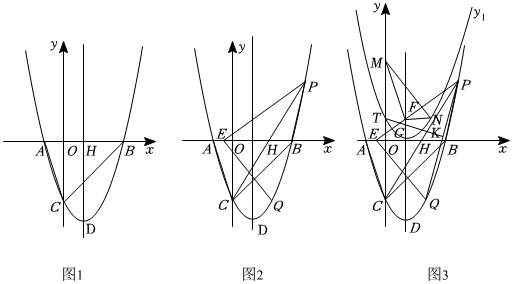
  组卷：41引用：1难度：0.2

  解析