如图1，二次函数y=ax2-2x+c（a≠0）的图象交x轴于点A（-1，0）、B（3，0）两点，与y轴交于点C，点D是抛物线的顶点，DH⊥x轴于点H连接AC，BC．
（1）求抛物线的解析式；
（2）如图2，点P是抛物线第一象限上一点，且满足△PBC的面积等于△ABC的面积．
①求点P的坐标；②点Q与点C关于直线DH对称，在x轴上找一点E，使得|EP-EQ|的值最大，求点E坐标以及这个最大值；
（3）如图3，在（2）问的条件下，设直线PE交y轴于点G，交直线DH于点F，y轴上有一定点M（0，4），点K为PQ的中点，连接MF，先将△MFG沿着直线MF翻折到△MFN，再将抛物线y=ax2-2x+c沿着其对称轴DH向上平移，得到抛物线y1，使得抛物线y1的图象刚好过点N，此时抛物线y1交y轴于点T，连接TK．请问在直线PE上是否存在一点Y，使得△TKY是直角三角形？若存在，请直接写出点Y的坐标；若不存在，请说明理由．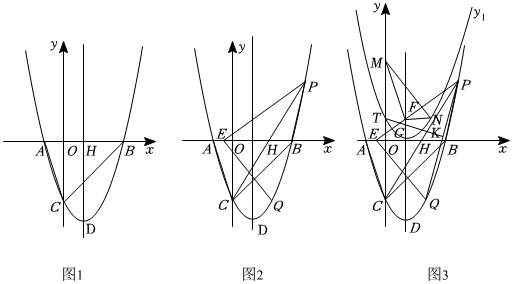
【考点】二次函数综合题．
【答案】（1）y=x2-2x-3；
（2）①P（4，5）；②E（-1，0），|EP-EQ|的最大值为2；
（3）在直线PE上存在点Y，使得△TKY是直角三角形，点Y的坐标为（-，）或（，）或（0，1）或（，）．
（2）①P（4，5）；②E（-1，0），|EP-EQ|的最大值为2
2
（3）在直线PE上存在点Y，使得△TKY是直角三角形，点Y的坐标为（-
12
575
563
575
75
23
98
23
81
50
131
50
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：41引用：1难度：0.2
相似题
-
1．如图，在平面直角坐标系xOy中，抛物线y=ax2+2x+c（a≠0）与x轴交于点A（-1，0）和点B，交y轴于点C（0，3），顶点为D．
（1）求抛物线解析式；
（2）点E为线段BD上的一个动点，作EF⊥x轴于点F，连接OE，当△OEF面积最大时．求点E的坐标；
（3）G是第四象限内抛物线上一点，过点G作GH⊥x轴于点H，交直线BD于点K、且OH=GK，作直线AG．145
①点G的坐标是 ；
②P为直线AG上方抛物线上一点，过点P作PQ⊥AG于点Q，取点M（0，），点N为平面内一点，若四边形MPNQ是菱形，请直接写出菱形的边长．74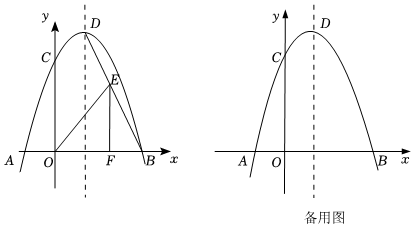
发布：2025/5/25 5:30:2组卷：984引用：2难度：0.1 -
2．如图，抛物线y=-
x2+bx+c过点A（3，2），且与直线y=-x+12交于B、C两点，点B的坐标为（4，m）．72
（1）求抛物线的解析式；
（2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；
（3）设点M为抛物线的顶点，在y轴上是否存在点Q，使∠AQM=45°？若存在，求点Q的坐标；若不存在，请说明理由．发布：2025/5/25 6:0:1组卷：5787引用：26难度：0.1 -
3．如图，已知抛物线y=ax2+bx+4（a≠0）与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为直线x=
．52
（1）求抛物线的解析式；
（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由；
（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE=2∠ODQ．在y轴上是否存在点F，使得△BEF为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．
发布：2025/5/25 6:0:1组卷：3234引用：20难度：0.4
